Hoe Bereken Je De Straal

Heb je je ooit afgevraagd hoe je de straal van een cirkel berekent? Of het nu gaat om het perfect positioneren van een pizza in een doos, het ontwerpen van een logo, of simpelweg het begrijpen van de wiskunde achter alledaagse objecten, de straal speelt een cruciale rol. Deze gids is bedoeld voor iedereen – van scholieren die worstelen met meetkunde tot hobbyisten die een nauwkeurige cirkel nodig hebben – en biedt een heldere en toegankelijke uitleg over het berekenen van de straal.

Wat is de Straal eigenlijk?

Voordat we in de berekeningen duiken, laten we eerst definiëren wat de straal precies is. De straal (aangeduid met r) is de afstand van het middelpunt van een cirkel tot een willekeurig punt op de omtrek van die cirkel. Het is de halve diameter (de lijn die door het middelpunt van de cirkel loopt en beide zijden van de cirkel raakt). Het begrijpen van deze basisdefinitie is essentieel voor alle volgende stappen.

De Straal Berekenen: Verschillende Methoden

Er zijn verschillende manieren om de straal van een cirkel te berekenen, afhankelijk van welke informatie je al hebt. We zullen de meest voorkomende methoden behandelen:

1. Van Diameter naar Straal

Dit is de meest eenvoudige methode. Zoals eerder vermeld, is de straal de helft van de diameter. Dus, als je de diameter (d) weet, kun je de straal (r) berekenen met de volgende formule:

r = d / 2

Voorbeeld: Stel, de diameter van een taart is 30 cm. De straal van de taart is dan 30 cm / 2 = 15 cm.

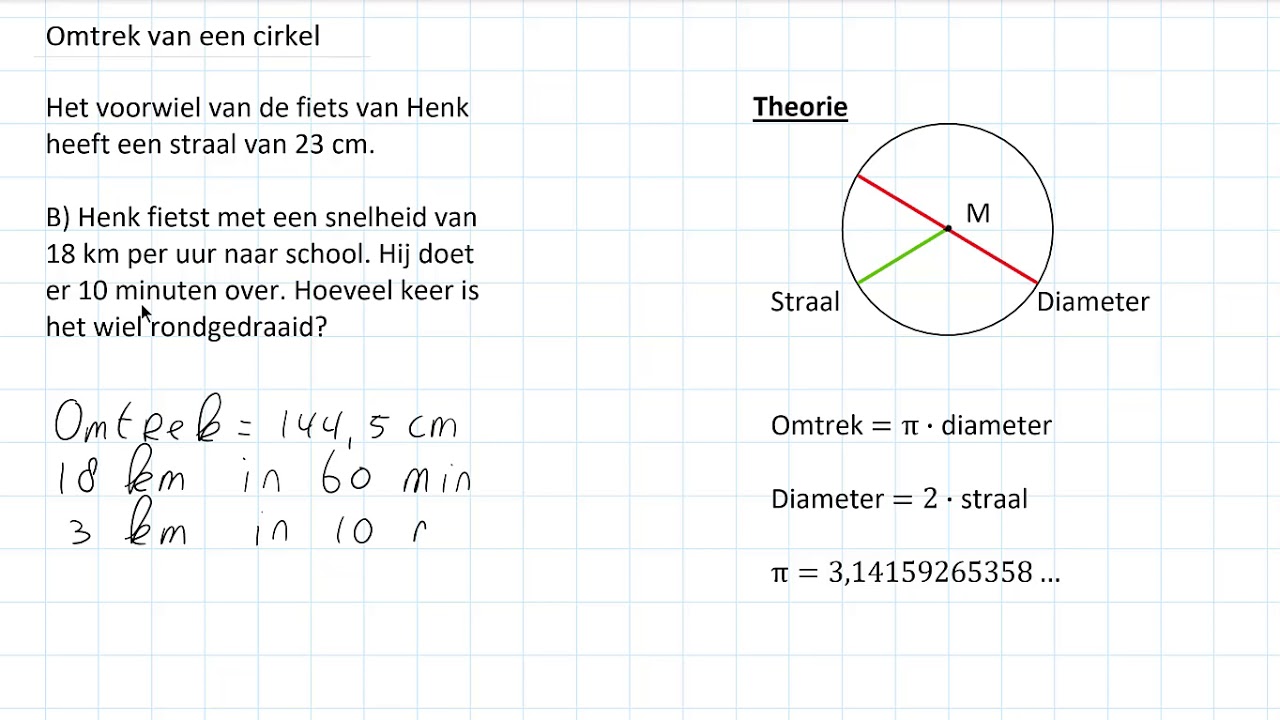
2. Van Omtrek naar Straal

De omtrek (C) van een cirkel is de afstand rond de cirkel. De formule voor de omtrek is:

C = 2 * π * r

Waar π (pi) een constante is, ongeveer gelijk aan 3.14159. Om de straal te berekenen als je de omtrek weet, kun je de formule herschrijven:

r = C / (2 * π)

Voorbeeld: Stel dat de omtrek van een zwembad 25 meter is. De straal van het zwembad is dan 25 meter / (2 * 3.14159) ≈ 3.98 meter.

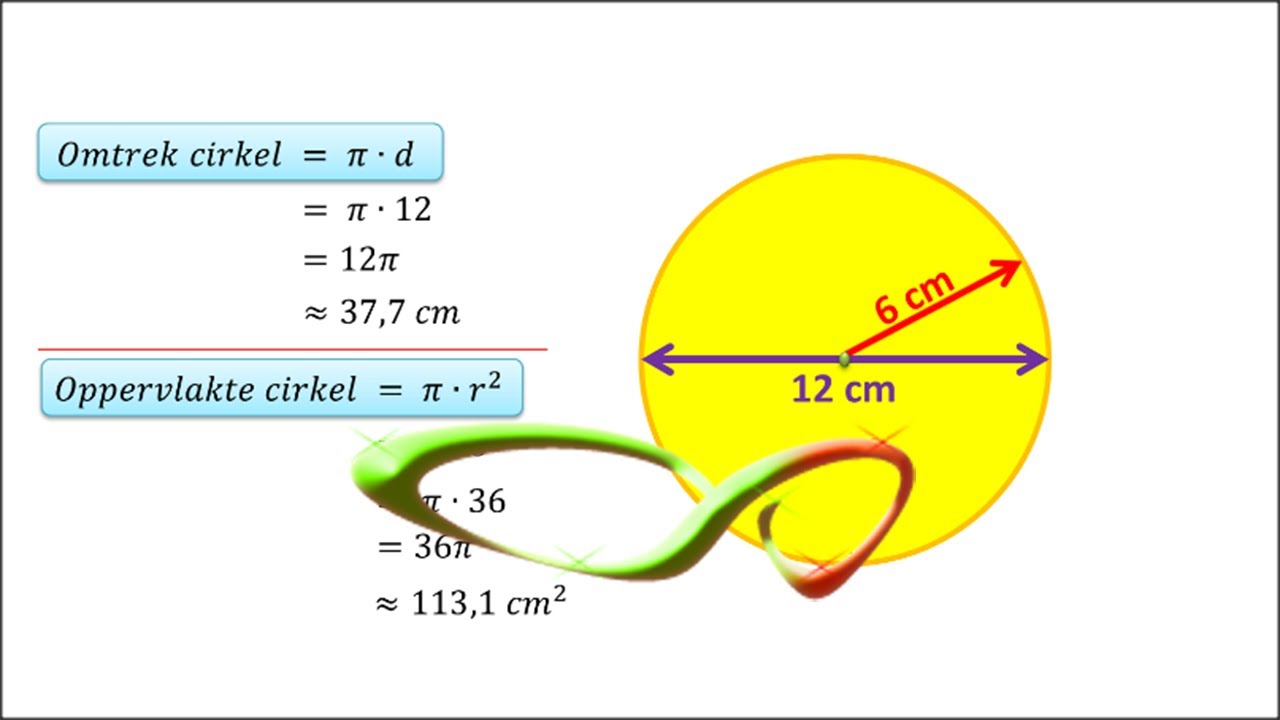
3. Van Oppervlakte naar Straal

De oppervlakte (A) van een cirkel is de ruimte die de cirkel inneemt. De formule voor de oppervlakte is:

A = π * r²

Om de straal te berekenen als je de oppervlakte weet, kun je de formule herschrijven:

r = √(A / π)

Waar √(x) de vierkantswortel van x betekent.

Voorbeeld: Stel dat de oppervlakte van een pizzabodem 200 cm² is. De straal van de pizzabodem is dan √(200 cm² / 3.14159) ≈ 7.98 cm.

4. Via Pythagoras (voor een Cirkelsegment)

Soms heb je geen diameter, omtrek of oppervlakte, maar wel informatie over een cirkelsegment – een stuk van een cirkel dat wordt begrensd door een boog en een koorde. In dit geval kan de stelling van Pythagoras helpen. Stel dat je de lengte van de koorde (c) en de hoogte van het segment (h) kent. De straal (r) kan dan worden berekend met de volgende formule:

r = (c² / (8 * h)) + (h / 2)

Voorbeeld: Stel dat de koorde van een cirkelsegment 10 cm is en de hoogte 2 cm. De straal van de cirkel is dan (10² / (8 * 2)) + (2 / 2) = (100 / 16) + 1 = 6.25 + 1 = 7.25 cm.

Praktische Toepassingen van de Straal

Het berekenen van de straal is niet alleen een theoretische oefening. Het heeft tal van praktische toepassingen in het dagelijks leven en in verschillende vakgebieden:

• Bouwkunde en Architectuur: Voor het ontwerpen van ronde structuren, zoals koepels en bogen.
• Engineering: Voor het berekenen van de grootte en afmetingen van roterende onderdelen, zoals wielen en tandwielen.
• Grafisch Ontwerp: Voor het creëren van logo's en illustraties met nauwkeurige cirkels.
• Koken: Voor het bepalen van de grootte van pannen en bakvormen.
• Wiskunde en Natuurkunde: Als basis voor meer geavanceerde berekeningen en modellen.
• Gaming en Virtual Reality: Voor het ontwerpen van virtuele omgevingen en objecten.

Tips en Trucs voor het Berekenen van de Straal

Hier zijn een paar handige tips en trucs om het berekenen van de straal makkelijker te maken:

• Gebruik een Rekenmachine: Vooral bij complexere berekeningen met π (pi) is een rekenmachine onmisbaar.
• Controleer je Eenheden: Zorg ervoor dat alle metingen in dezelfde eenheden zijn (bijvoorbeeld, alles in centimeters of alles in meters) voordat je begint met rekenen.
• Maak een Schets: Een visuele weergave van de cirkel en de gegeven informatie kan helpen om de situatie beter te begrijpen.
• Wees Nauwkeurig: Gebruik zoveel mogelijk decimalen van π (pi) als je precisie nodig hebt. De meeste rekenmachines hebben een π knop.
• Oefen Regelmatig: Zoals met alle wiskundige vaardigheden, geldt ook hier: oefening baart kunst. Probeer verschillende voorbeelden en scenario's om je begrip te vergroten.

Veelgemaakte Fouten en Hoe Ze te Vermijden

Het is makkelijk om fouten te maken bij het berekenen van de straal. Hier zijn enkele veelgemaakte fouten en hoe je ze kunt vermijden:

• Diameter en Straal Verwarren: Zorg ervoor dat je de diameter en de straal niet door elkaar haalt. Onthoud dat de straal de helft van de diameter is.
• Verkeerde Formule Gebruiken: Gebruik de juiste formule voor de gegeven informatie (bijvoorbeeld, gebruik de formule voor omtrek als je de omtrek weet, en de formule voor oppervlakte als je de oppervlakte weet).
• Verkeerde Eenheden: Werk altijd met consistente eenheden.
• Afrondingsfouten: Vermijd te vroeg afronden tijdens de berekening. Rond pas af aan het einde van de berekening, om de nauwkeurigheid te maximaliseren.
• π (Pi) Verkeerd Gebruiken: Gebruik de π knop op je rekenmachine of een nauwkeurige waarde van π (bijvoorbeeld 3.14159) in plaats van een afgeronde waarde zoals 3.14.

Samenvatting en Conclusie

Het berekenen van de straal van een cirkel is een fundamentele vaardigheid met talloze toepassingen. Door de verschillende methoden te begrijpen – van diameter, omtrek, oppervlakte, of via de stelling van Pythagoras – kun je de straal in diverse situaties nauwkeurig bepalen. Onthoud de basisdefinities, oefen regelmatig, en vermijd de veelgemaakte fouten die we hebben besproken. Met deze kennis ben je goed uitgerust om elke cirkelvormige uitdaging aan te gaan!

Of je nu een student bent die aan zijn wiskundehuiswerk werkt, een professional die een project ontwerpt, of gewoon iemand die geïnteresseerd is in de wereld om je heen, het begrijpen van de straal zal je zeker van pas komen. Dus ga eropuit en omarm de kracht van de cirkel!