Hoe Bereken Je Percentage Uit

Heb je ooit in een winkel gestaan, twijfelend over de werkelijke korting op dat ene item? Of ben je bezig met je budget en vraag je je af welk percentage van je inkomen naar huur gaat? Het berekenen van percentages is een essentiële vaardigheid die we in veel aspecten van ons dagelijks leven gebruiken. Deze vaardigheid stelt ons in staat om data te begrijpen, beslissingen te nemen en de wereld om ons heen beter te interpreteren. Dit artikel is bedoeld voor iedereen die de basis van het berekenen van percentages wil begrijpen of zijn/haar kennis wil opfrissen. We zullen de formules en methoden stap voor stap uitleggen, zodat je na het lezen van dit artikel zelfverzekerd percentages kunt berekenen.

Wat is een percentage?

Een percentage is een manier om een verhouding uit te drukken als een breuk van 100. Het woord "percentage" komt van het Latijnse "per centum," wat "per honderd" betekent. Een percentage geeft aan welk deel van een geheel vertegenwoordigd wordt. We gebruiken het percentage symbool, %, om aan te geven dat een getal als een percentage wordt uitgedrukt.

Denk erover na: 50% is hetzelfde als 50/100, wat weer gelijk is aan 1/2. Het is een andere manier om dezelfde informatie te presenteren, maar vaak handiger en intuïtiever.

De basisformule voor het berekenen van een percentage

De meest fundamentele formule voor het berekenen van een percentage is als volgt:

Percentage (%) = (Deel / Geheel) x 100

Laten we deze formule eens ontleden:

Deel: Dit is het specifieke aantal of de hoeveelheid waarover je het percentage wilt berekenen.
Geheel: Dit is het totale aantal of de totale hoeveelheid waaruit het deel afkomstig is.
x 100: We vermenigvuldigen de breuk (Deel / Geheel) met 100 om het resultaat als een percentage uit te drukken.

Voorbeeld 1: Korting berekenen

Stel, je wilt een trui kopen die oorspronkelijk €50 kost, maar nu met €10 is afgeprijsd. Hoeveel procent korting krijg je?

Deel: €10 (de korting)
Geheel: €50 (de oorspronkelijke prijs)

Percentage (%) = (10 / 50) x 100 = 0.2 x 100 = 20%

Je krijgt dus 20% korting.

Voorbeeld 2: Cijfer voor een toets

Je hebt een toets gemaakt met 80 vragen en je hebt er 64 goed beantwoord. Wat is je score in percentage?

Deel: 64 (het aantal correcte antwoorden)
Geheel: 80 (het totale aantal vragen)

Percentage (%) = (64 / 80) x 100 = 0.8 x 100 = 80%

Je score is 80%.

Verschillende toepassingen van het berekenen van percentages

Zoals we al eerder aangaven, komt het berekenen van percentages in veel verschillende situaties van pas. Laten we er een paar verkennen:

1. Financiën en Budgettering

Percentages zijn cruciaal voor het beheren van je persoonlijke financiën. Je kunt berekenen:

Welk percentage van je inkomen je aan verschillende uitgaven besteedt (huur, boodschappen, transport, entertainment).
De rente die je betaalt op een lening of verdient op een spaarrekening.
De winst of verlies van een investering in percentage.

2. Verkoop en Marketing

Bedrijven gebruiken percentages om:

Verkoopgroei te meten.
Marktaandeel te bepalen.
De effectiviteit van marketingcampagnes te analyseren.
Kortingen te berekenen (zoals we in het voorbeeld hierboven zagen).

3. Statistiek en Data-analyse

In de statistiek worden percentages gebruikt om data te presenteren en te interpreteren. Bijvoorbeeld:

Het percentage van de bevolking dat een bepaalde aandoening heeft.
Het percentage van de stemmen dat een politieke partij heeft behaald.
De verandering in een bepaalde statistiek over een bepaalde periode.

4. Onderwijs

Studenten gebruiken percentages om hun prestaties te evalueren. Denk aan:

Het berekenen van hun cijfer voor een vak.
Het bepalen van hun slaagkans voor een examen.
Het vergelijken van hun prestaties met die van andere studenten (in percentage).

Percentage verandering berekenen

Soms wil je weten hoeveel iets is veranderd in percentage. Dit wordt de percentage verandering genoemd. De formule hiervoor is:

Percentage verandering (%) = ((Nieuwe waarde - Oude waarde) / Oude waarde) x 100

Voorbeeld: Prijsstijging

Stel dat de prijs van een brood van €2 naar €2.50 is gestegen. Wat is de percentage verandering?

Nieuwe waarde: €2.50
Oude waarde: €2.00

Percentage verandering (%) = ((2.50 - 2.00) / 2.00) x 100 = (0.50 / 2.00) x 100 = 0.25 x 100 = 25%

De prijs van het brood is met 25% gestegen.

Een negatieve percentage verandering

Het is belangrijk te beseffen dat een percentage verandering ook negatief kan zijn. Dit geeft aan dat er een afname is in de waarde. Bijvoorbeeld:

Stel dat de prijs van een product van €100 naar €80 is gedaald. Wat is de percentage verandering?

Nieuwe waarde: €80
Oude waarde: €100

Percentage verandering (%) = ((80 - 100) / 100) x 100 = (-20 / 100) x 100 = -0.20 x 100 = -20%

De prijs van het product is met 20% gedaald.

Tips en Tricks voor het berekenen van percentages

Hier zijn een paar handige tips en tricks die het berekenen van percentages makkelijker kunnen maken:

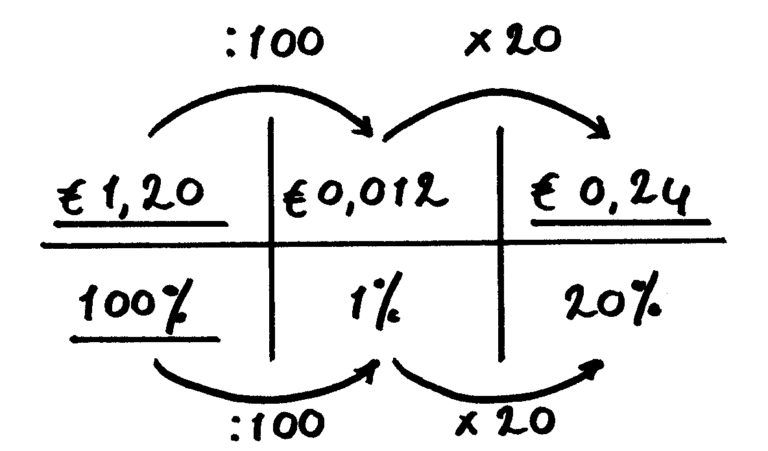
Omzetten naar een decimaal: Deel het percentage door 100 om het om te zetten in een decimaal. Bijvoorbeeld, 25% = 25/100 = 0.25. Dit maakt het makkelijker om mee te rekenen.
Gebruik een rekenmachine: Moderne rekenmachines (zelfs die op je telefoon) hebben een percentage-knop (%). Leer hoe je deze gebruikt om tijd te besparen.
Schatting: Voordat je gaat rekenen, probeer een schatting te maken van het antwoord. Dit helpt je om te controleren of je eindresultaat redelijk is. Bijvoorbeeld, als je 51% van 100 berekent, weet je dat het antwoord net boven de 50 zal liggen.
Oefening baart kunst: Hoe meer je oefent met het berekenen van percentages, hoe sneller en zelfverzekerder je zult worden. Zoek online naar oefeningen of bedenk zelf voorbeelden uit je dagelijks leven.

Het belang van context

Het is cruciaal om de context te begrijpen wanneer je met percentages werkt. Een percentage op zichzelf kan misleidend zijn als je de context niet kent. Bijvoorbeeld:

Absoluut versus Relatief: Stel je voor dat twee bedrijven hun omzet met 10% zien stijgen. Bedrijf A had een omzet van €10.000, terwijl Bedrijf B een omzet van €1.000.000 had. Hoewel de percentage stijging hetzelfde is, is de absolute stijging in omzet veel groter voor Bedrijf B.
Base Rate Neglect: Wees voorzichtig met conclusies trekken op basis van percentages als je de basis (base rate) niet kent. Een medicijn dat in 99% van de gevallen werkt, klinkt geweldig. Maar als de aandoening in de eerste plaats al vanzelf geneest in 98% van de gevallen, is het medicijn misschien niet zo indrukwekkend als het lijkt.

Conclusie

Het berekenen van percentages is een fundamentele vaardigheid die je in staat stelt om de wereld om je heen beter te begrijpen en weloverwogen beslissingen te nemen. Door de basisformule te begrijpen, verschillende toepassingen te verkennen en de tips en tricks toe te passen, kun je zelfverzekerd percentages berekenen in diverse situaties. Of het nu gaat om het berekenen van kortingen, het analyseren van data of het beheren van je financiën, de kennis van percentages is onmisbaar. Blijf oefenen en toepassen wat je hebt geleerd, en je zult merken dat je steeds bekwamer wordt in deze waardevolle vaardigheid. Nu is het jouw beurt om deze kennis in de praktijk te brengen! Gebruik de volgende keer dat je een korting ziet of een statistiek leest, je nieuwe vaardigheden om de informatie te interpreteren en te begrijpen. Succes!