Hoek Van Een Driehoek Berekenen

Het berekenen van hoeken in een driehoek is een fundamentele vaardigheid in de geometrie en heeft talloze toepassingen in verschillende vakgebieden. Of je nu een student bent die de basisprincipes van de wiskunde leert, een architect die een gebouw ontwerpt, of een landmeter die land meet, het begrijpen hoe je de hoeken van een driehoek kunt bepalen is van cruciaal belang. Dit artikel biedt een uitgebreide uitleg van de verschillende methoden om hoeken in een driehoek te berekenen, zonder onnodige vereenvoudiging en met concrete voorbeelden.

Methoden voor het Berekenen van Hoek Van Een Driehoek

1. De Som van de Hoeken in een Driehoek

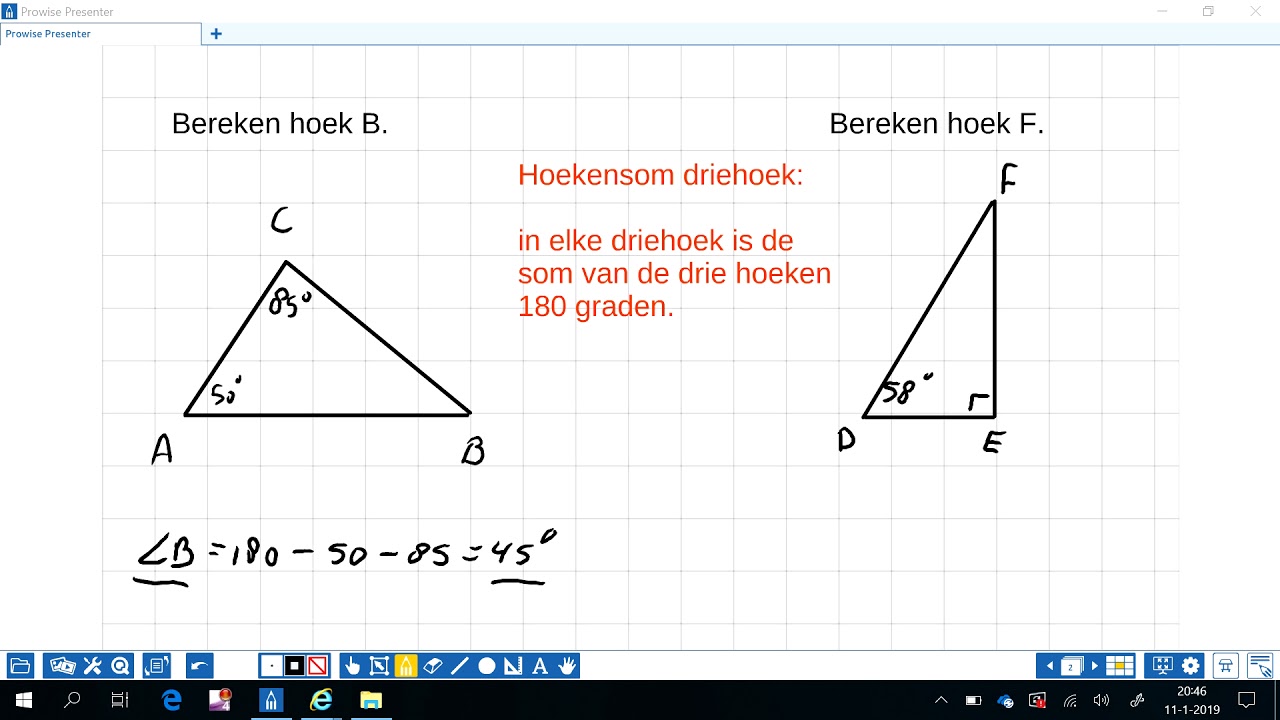
Een van de meest fundamentele principes van de geometrie is dat de som van de hoeken in elke driehoek altijd 180 graden is. Dit geldt voor alle soorten driehoeken: gelijkzijdige, gelijkbenige, scherphoekige, stomphoekige en rechthoekige. Dit principe is essentieel en vormt de basis voor veel andere berekeningen.

Als je de grootte van twee hoeken van een driehoek weet, kun je de derde hoek eenvoudig berekenen door de bekende hoeken van 180 graden af te trekken. Wiskundig kan dit worden weergegeven als: Hoek C = 180° - Hoek A - Hoek B, waarbij A, B en C de hoeken van de driehoek vertegenwoordigen.

Voorbeeld: Stel je voor dat je een driehoek hebt waarbij Hoek A 60 graden is en Hoek B 80 graden. Om Hoek C te vinden, trek je 60 en 80 af van 180: 180 - 60 - 80 = 40 graden. Dus, Hoek C is 40 graden.

2. Gebruik van Trigonometrische Functies

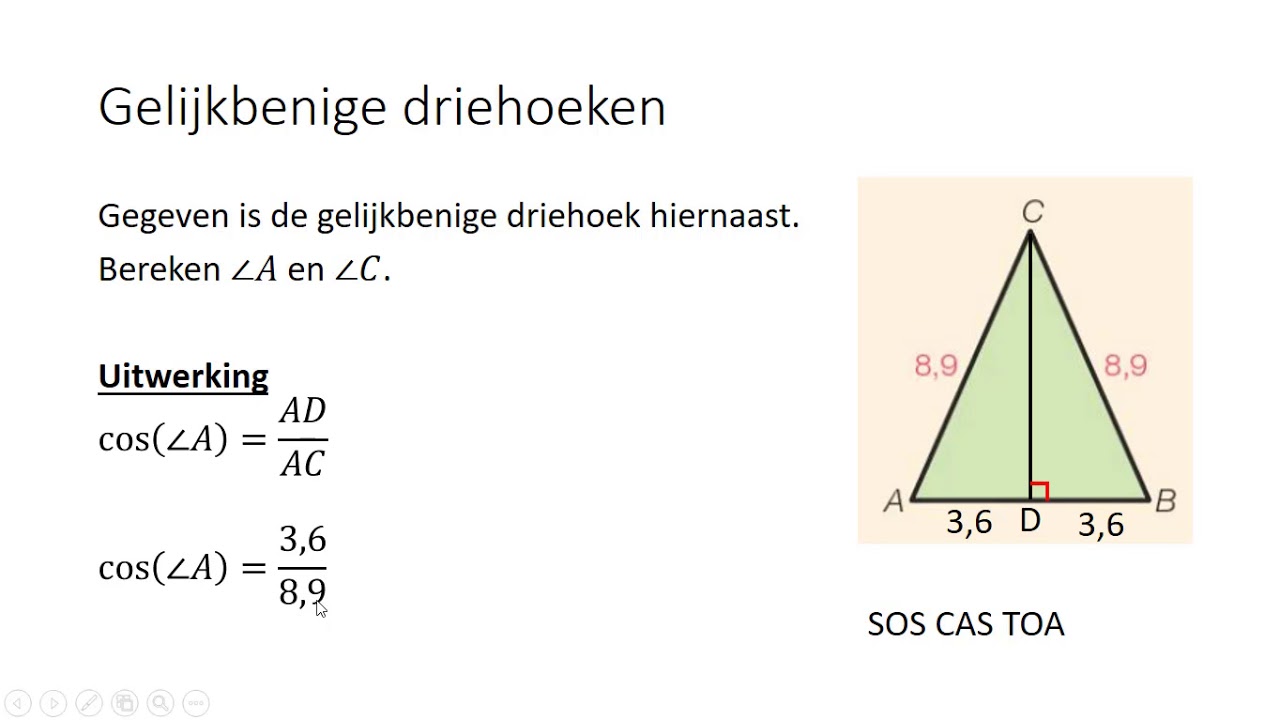
Wanneer je te maken hebt met een rechthoekige driehoek, kun je trigonometrische functies gebruiken om de hoeken te berekenen als je de lengte van de zijden kent. De belangrijkste trigonometrische functies zijn: sinus (sin), cosinus (cos) en tangens (tan). Deze functies relateren de hoeken van een rechthoekige driehoek aan de verhoudingen van de lengtes van de zijden.

Hier is een overzicht van hoe je deze functies kunt gebruiken:

• Sinus (sin): sin(hoek) = Overstaande zijde / Schuine zijde
• Cosinus (cos): cos(hoek) = Aanliggende zijde / Schuine zijde
• Tangens (tan): tan(hoek) = Overstaande zijde / Aanliggende zijde

Om de hoek zelf te vinden, gebruik je de inverse trigonometrische functies (arcsin, arccos, arctan), ook wel bekend als de inverse sinus, cosinus en tangens. De notatie hiervoor is meestal: sin^-1, cos^-1 en tan^-1.

Voorbeeld: Stel dat je een rechthoekige driehoek hebt waarbij de overstaande zijde 3 cm is en de schuine zijde 5 cm. Om de hoek te berekenen, gebruik je de sinus functie: sin(hoek) = 3/5 = 0.6. Vervolgens bereken je de inverse sinus: hoek = sin^-1(0.6) ≈ 36.87 graden.

3. De Cosinusregel

De cosinusregel is een krachtig hulpmiddel voor het berekenen van hoeken in elke driehoek, ongeacht of deze rechthoekig is of niet. De cosinusregel stelt een relatie vast tussen de lengtes van de zijden van een driehoek en de cosinus van een van de hoeken.

De cosinusregel kan in drie vormen worden geschreven, afhankelijk van welke hoek je wilt berekenen:

• a² = b² + c² - 2bc * cos(A) => cos(A) = (b² + c² - a²) / (2bc)
• b² = a² + c² - 2ac * cos(B) => cos(B) = (a² + c² - b²) / (2ac)
• c² = a² + b² - 2ab * cos(C) => cos(C) = (a² + b² - c²) / (2ab)

Waar a, b en c de lengtes van de zijden van de driehoek zijn en A, B en C de hoeken tegenover respectievelijk zijde a, zijde b en zijde c. Om de hoek zelf te vinden, neem je de inverse cosinus (arccos) van het resultaat.

Voorbeeld: Stel dat je een driehoek hebt met zijden van lengte a = 5, b = 7 en c = 8. Om Hoek A te berekenen, gebruik je de cosinusregel: cos(A) = (7² + 8² - 5²) / (2 * 7 * 8) = (49 + 64 - 25) / 112 = 88 / 112 ≈ 0.7857. Vervolgens bereken je de inverse cosinus: A = cos^-1(0.7857) ≈ 38.21 graden.

4. De Sinusregel

De sinusregel is een andere methode om hoeken en zijden in een driehoek te berekenen, en het is vooral handig wanneer je een paar (een hoek en de zijde ertegenover) kent en je een andere hoek of zijde wilt vinden. De sinusregel stelt dat de verhouding van de lengte van een zijde tot de sinus van de tegenoverliggende hoek constant is voor alle zijden en hoeken in de driehoek.

De formule voor de sinusregel is:

a / sin(A) = b / sin(B) = c / sin(C)

Waarbij a, b en c de lengtes van de zijden van de driehoek zijn, en A, B en C de hoeken tegenover respectievelijk zijde a, zijde b en zijde c.

Voorbeeld: Stel dat je een driehoek hebt waarbij zijde a = 10, Hoek A = 30 graden en Hoek B = 45 graden. Om zijde b te vinden, gebruik je de sinusregel: 10 / sin(30°) = b / sin(45°). Omdat sin(30°) = 0.5 en sin(45°) ≈ 0.707, krijg je 10 / 0.5 = b / 0.707. Dit vereenvoudigt tot 20 = b / 0.707, dus b = 20 * 0.707 ≈ 14.14.

Real-World Voorbeelden en Toepassingen

De principes van het berekenen van hoeken in driehoeken hebben talrijke praktische toepassingen. Hier zijn enkele voorbeelden:

• Architectuur: Architecten gebruiken trigonometrie en de kennis van hoeken om gebouwen te ontwerpen en ervoor te zorgen dat structuren stabiel en veilig zijn. Het berekenen van de hoeken van daken, muren en andere elementen is essentieel voor het bouwen van duurzame en esthetisch aantrekkelijke gebouwen.
• Landmeten: Landmeters gebruiken trigonometrie om land te meten en kaarten te maken. Door de hoeken en afstanden tussen verschillende punten te meten, kunnen ze nauwkeurige kaarten en terreinmodellen maken.
• Navigatie: In de navigatie worden hoeken en trigonometrie gebruikt om posities te bepalen en routes te plannen. Zowel op zee als in de lucht is een goed begrip van hoeken essentieel voor een veilige en efficiënte navigatie.
• Engineering: Ingenieurs gebruiken de principes van het berekenen van hoeken in de constructie van bruggen, tunnels en andere infrastructurele projecten. De juiste hoeken en afstanden zijn cruciaal voor de structurele integriteit van deze projecten.
• Astronomie: Astronomen gebruiken trigonometrie om de afstanden tot sterren en planeten te bepalen. Door de hoeken te meten waaronder sterren worden waargenomen vanaf verschillende punten op aarde, kunnen ze de afstanden tot deze hemellichamen berekenen.

Een concreet voorbeeld is de constructie van een houten schuur. Om een stevig dak te bouwen, moet de hoek van de dakhelling correct worden berekend. Als de hoek te steil is, kan de schuur instabiel worden in harde wind. Als de hoek te flauw is, kan er water blijven staan en lekkage veroorzaken. Door trigonometrie te gebruiken, kan de juiste hoek worden bepaald om de stabiliteit en waterdichtheid van het dak te garanderen. Dit omvat het meten van de breedte van de schuur (aanliggende zijde) en de gewenste hoogte van de nok (overstaande zijde) en vervolgens het gebruik van de tangensfunctie om de hoek te berekenen: tan(hoek) = overstaande zijde / aanliggende zijde.

Conclusie

Het berekenen van hoeken in een driehoek is een essentiële vaardigheid met brede toepassingen in verschillende disciplines. Door de basisprincipes te begrijpen, zoals de som van de hoeken in een driehoek, trigonometrische functies, de cosinusregel en de sinusregel, kun je een breed scala aan problemen oplossen. Of je nu een professional bent die deze vaardigheden in zijn werk gebruikt, of een student die de basisprincipes van wiskunde leert, een diepgaand begrip van hoe je hoeken in een driehoek kunt berekenen, is van onschatbare waarde.

Oefen regelmatig met verschillende soorten problemen om je vaardigheden te verbeteren en een beter begrip te krijgen van de concepten. Er zijn talloze online bronnen en oefeningen beschikbaar om je te helpen. Dus, ga aan de slag en ontdek de fascinerende wereld van driehoeken en hun hoeken!