Hoeveel Graden Is Een Gelijkzijdige Driehoek

Heb je je ooit afgevraagd hoeveel graden er in een gelijkzijdige driehoek zitten? Misschien ben je een student die worstelt met meetkunde, of iemand die gewoon nieuwsgierig is naar de wereld om je heen. Meetkunde kan soms intimiderend lijken, maar wees gerust, de antwoorden liggen vaak in verrassend simpele concepten. Dit artikel is er om je te helpen dit basisconcept te begrijpen.

De Basis: Driehoeken en Graden

Laten we beginnen met de basis. Een driehoek is een geometrische figuur met drie zijden en drie hoeken. Een fundamenteel principe is dat de som van de hoeken in elke driehoek, ongeacht de vorm, altijd 180 graden is. Dit is een onwrikbaar feit in de Euclidische meetkunde.

Waarom is dit belangrijk? Omdat het ons de sleutel geeft tot het begrijpen van gelijkzijdige driehoeken.

Wat is een Gelijkzijdige Driehoek?

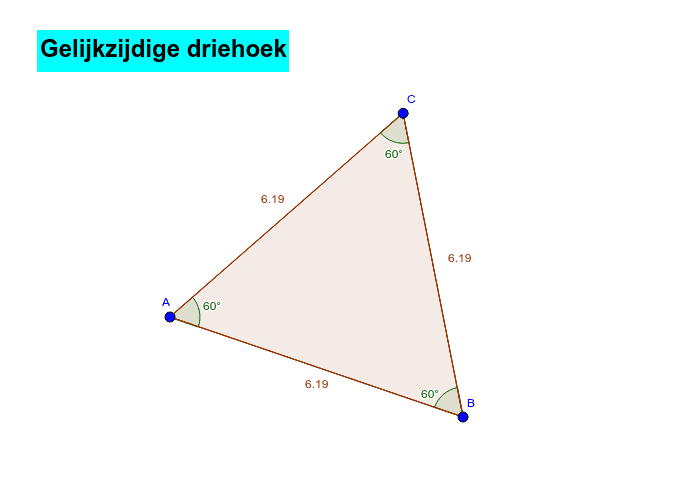
Een gelijkzijdige driehoek is een bijzondere soort driehoek. Hij wordt gekenmerkt door twee belangrijke eigenschappen:

• Alle drie de zijden zijn even lang.
• Alle drie de hoeken zijn even groot.

Deze gelijkheid van zijden en hoeken maakt de gelijkzijdige driehoek zo'n elegant en voorspelbaar figuur.

De Berekening: Hoeveel Graden?

Nu komen we tot de kern van de vraag: Hoeveel graden heeft elke hoek in een gelijkzijdige driehoek? We weten dat de som van alle hoeken in een driehoek 180 graden is. En we weten dat in een gelijkzijdige driehoek alle hoeken gelijk zijn. Dus, om de waarde van één hoek te vinden, kunnen we een simpele berekening uitvoeren:

1. Stel de waarde van één hoek voor als x.

2. Omdat er drie hoeken zijn, is de totale som 3x.

3. We weten dat 3x = 180 graden.

4. Om x te vinden, delen we beide zijden van de vergelijking door 3: x = 180 / 3.

5. Dus, x = 60 graden.

Daarom is elke hoek in een gelijkzijdige driehoek 60 graden. Dit is altijd waar.

Waarom is dit belangrijk? De Impact in de Wereld

Je vraagt je misschien af: "Waarom zou ik dit eigenlijk moeten weten?" Het antwoord is dat meetkunde, en gelijkzijdige driehoeken in het bijzonder, overal om ons heen voorkomen. Denk aan:

• Architectuur: Veel structuren, zoals bruggen en daken, gebruiken driehoeken voor hun sterkte en stabiliteit. De perfecte hoeken van een gelijkzijdige driehoek kunnen helpen bij het ontwerpen van gelijkmatige en sterke structuren.
• Engineering: Ingenieurs gebruiken geometrische principes om machines, apparaten en voertuigen te ontwerpen. De hoeken van een gelijkzijdige driehoek kunnen cruciaal zijn bij het bepalen van de juiste afmetingen en verhoudingen voor een bepaald onderdeel.
• Kunst en Design: Van mozaïeken tot logo's, gelijkzijdige driehoeken worden vaak gebruikt in kunst en design vanwege hun visuele aantrekkingskracht en symmetrie.
• Natuur: Je vindt drievoudige symmetrie (wat vaak op gelijkzijdige driehoeken berust) terug in natuurlijke structuren, zoals honingraten en bepaalde kristallen.

Het begrijpen van basale meetkunde stelt je in staat om de wereld om je heen beter te begrijpen en te waarderen.

Mogelijke Verwarring en Tegenargumenten

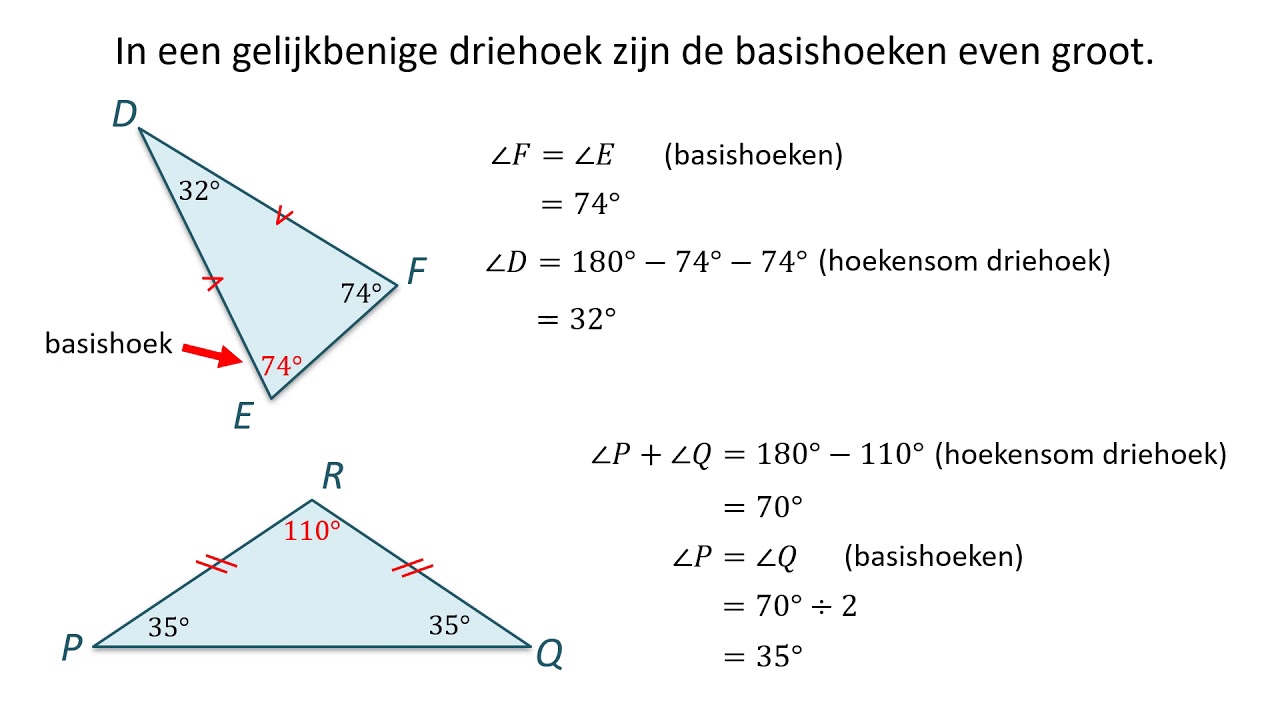
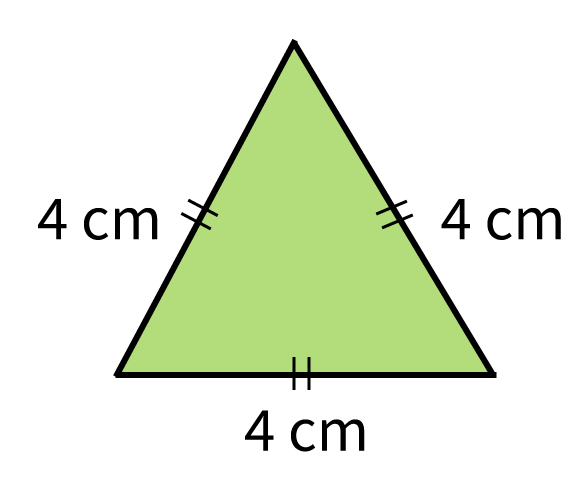
Soms ontstaat er verwarring tussen gelijkzijdige en gelijkbenige driehoeken. Een gelijkbenige driehoek heeft twee gelijke zijden en twee gelijke hoeken. Het is niet noodzakelijk dat alle drie de hoeken gelijk zijn. Een gelijkzijdige driehoek *is* altijd gelijkbenig, maar een gelijkbenige driehoek is *niet* altijd gelijkzijdig.

Er zijn ook mensen die beweren dat Euclidische meetkunde niet de enige geldige vorm van meetkunde is. In niet-Euclidische meetkunde kunnen de regels anders zijn en de som van de hoeken in een driehoek kan anders zijn dan 180 graden. Hoewel dit waar is, is Euclidische meetkunde nog steeds de meest gebruikte en relevante vorm van meetkunde in de meeste praktische toepassingen van het dagelijks leven.

Oplossingen en Verdere Stappen

Als je worstelt met meetkunde, zijn hier enkele tips:

• Oefen regelmatig: Meetkunde vereist oefening. Werk door problemen, teken diagrammen en visualiseer concepten.
• Gebruik hulpmiddelen: Er zijn veel online bronnen, tutorials en apps beschikbaar om je te helpen meetkunde te leren.
• Zoek hulp: Aarzel niet om hulp te vragen aan je leraar, een tutor of een klasgenoot.
• Maak het leuk: Probeer meetkunde te relateren aan je interesses. Bijvoorbeeld, als je van gamen houdt, zoek dan naar games die meetkundige concepten gebruiken.

Verdieping van de Kennis

Wil je dieper in de meetkunde duiken? Overweeg dan de volgende onderwerpen:

• Pythagoras' stelling: Een fundamenteel principe in de meetkunde dat de relatie tussen de zijden van een rechthoekige driehoek beschrijft.
• Trigonometrie: De studie van de relaties tussen de hoeken en zijden van driehoeken.
• Analytische meetkunde: Het gebruik van algebra om meetkundige problemen op te lossen.

Conclusie

De hoeken van een gelijkzijdige driehoek zijn elk 60 graden. Dit is een fundamenteel concept in meetkunde dat relevant is voor veel aspecten van ons leven, van architectuur tot kunst. Door dit basisprincipe te begrijpen, open je een wereld van mogelijkheden en kun je de wereld om je heen beter begrijpen.

Nu je dit weet, hoe ga je deze kennis gebruiken om de wereld om je heen te verkennen en te begrijpen? Welke meetkundige vormen zie je in je dagelijkse leven, en welke principes zijn daarop van toepassing?