Tan Sin Cos Or Cos Sin
Heb je je ooit afgevraagd hoe die sinus, cosinus en tangens nu precies werken? Misschien heb je ze wel eens in de wiskundeles gezien en dacht je: "Waar heb ik dit ooit voor nodig?". Je bent niet de enige. Veel mensen worstelen met goniometrie, en het kan voelen alsof je een geheime code probeert te ontcijferen.
Maar vrees niet! Dit artikel is geschreven om je te helpen. We gaan deze functies stap voor stap bekijken, zodat je ze niet alleen begrijpt, maar ook kunt toepassen in de echte wereld. Geen moeilijke wiskundige taal, gewoon duidelijke uitleg en praktische voorbeelden.
Wat zijn Sinus, Cosinus en Tangens eigenlijk?
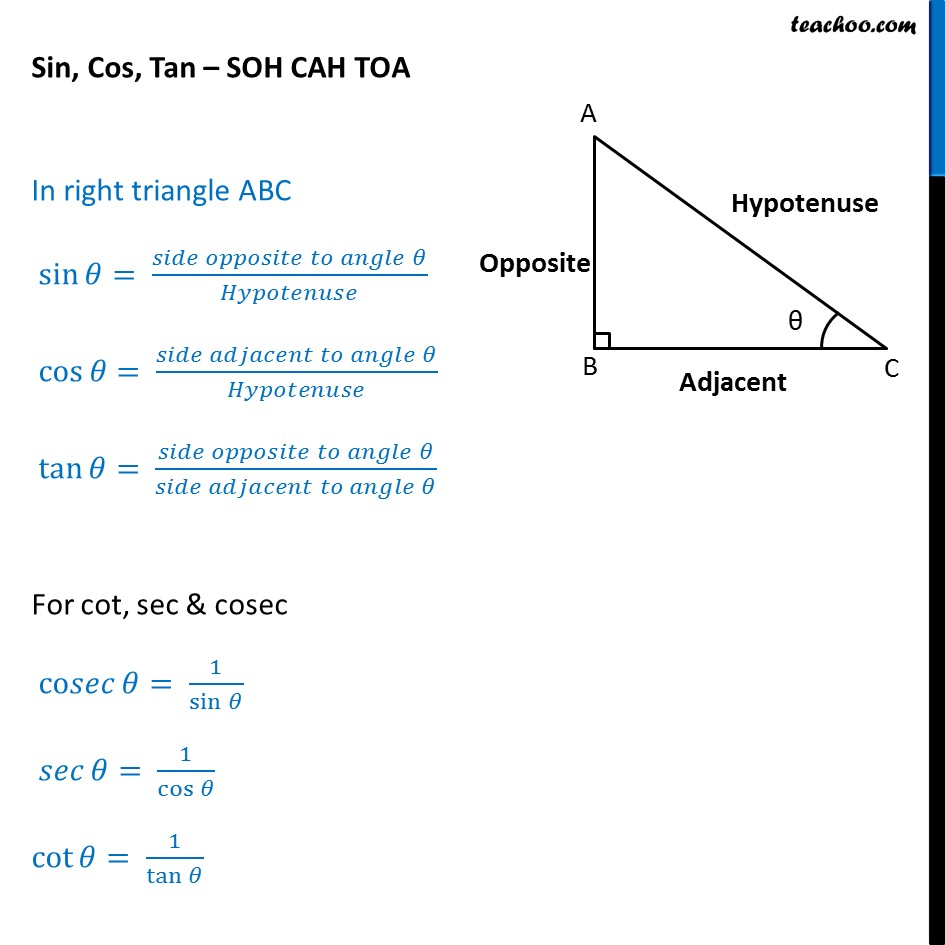
Laten we beginnen met de basis. Sinus, cosinus en tangens (vaak afgekort tot sin, cos en tan) zijn trigonometrische functies. Dat klinkt ingewikkeld, maar het betekent eigenlijk gewoon dat ze een relatie beschrijven tussen de hoeken en de zijden van een rechthoekige driehoek.
Een rechthoekige driehoek is een driehoek met één hoek van 90 graden (een rechte hoek). De langste zijde, tegenover de rechte hoek, noemen we de hypotenusa. De andere twee zijden noemen we de aanliggende en de overstaande zijde, afhankelijk van de hoek die we bekijken.
Onthoud de volgende definities:
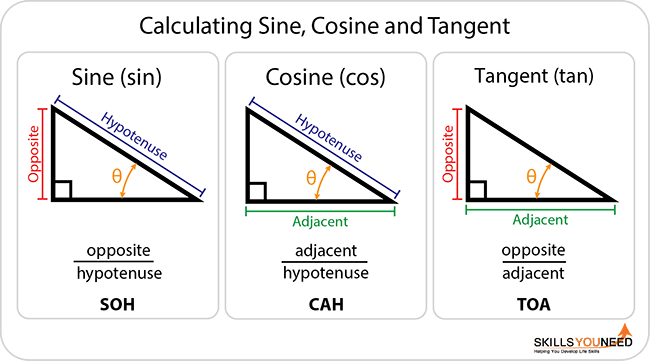
- Sinus (sin): Overstaande zijde / Hypotenusa
- Cosinus (cos): Aanliggende zijde / Hypotenusa
- Tangens (tan): Overstaande zijde / Aanliggende zijde
Een handig ezelsbruggetje om dit te onthouden is "SOS CAS TOA":
- Sinus = Overstaande / Hypotenusa
- Cosinus = Aanliggende / Hypotenusa
- Tangens = Overstaande / Aanliggende
Hoe gebruik je ze?
Stel je voor: je staat voor een boom en je wilt weten hoe hoog hij is. Je kunt niet zomaar een meetlint gebruiken, maar je kunt wel de hoek meten waaronder je de top van de boom ziet (de elevatiehoek) en de afstand van je tot de boom. Met deze informatie kun je de hoogte van de boom berekenen met behulp van de tangens.
Voorbeeld:
Je staat 20 meter van de boom af. De elevatiehoek is 40 graden. De tangens van 40 graden is ongeveer 0.839. Dus, de hoogte van de boom is:
Hoogte = Afstand * tan(hoek) = 20 meter * 0.839 = 16.78 meter.
Zo zie je, de tangens helpt je om de hoogte van de boom te bepalen zonder hem daadwerkelijk te beklimmen!
Waar worden Sinus, Cosinus en Tangens gebruikt?
Deze functies zijn veel breder toepasbaar dan je misschien denkt. Hier zijn een paar voorbeelden:
- Navigatie: Schepen en vliegtuigen gebruiken goniometrie om hun positie te bepalen en hun koers te berekenen. GPS-systemen zijn er ook sterk op gebaseerd.
- Architectuur en Engineering: Bij het ontwerpen van gebouwen en bruggen worden sinus, cosinus en tangens gebruikt om hoeken, afstanden en krachten te berekenen.
- Natuurkunde: Golfbewegingen (zoals geluid en licht) kunnen worden beschreven met sinus- en cosinusfuncties.
- Computer graphics: Bij het maken van 3D-animaties en games worden deze functies gebruikt om objecten te roteren, te schalen en te transformeren.
- Muziek: Geluidsgolven zijn sinusgolven. Analyse en synthese van geluid maakt gebruik van goniometrische functies.
Een studie van de Universiteit van Californië, Berkeley, toonde aan dat een sterk begrip van goniometrie essentieel is voor succes in STEM-velden (Science, Technology, Engineering, and Mathematics). Het is een fundamentele bouwsteen voor veel complexe concepten.
Sinus en Cosinus in Circulaire Bewegingen
Een van de meest fundamentele toepassingen is in de beschrijving van circulaire bewegingen. Denk aan een draaimolen. De positie van een zitje op de draaimolen kan worden beschreven met behulp van sinus en cosinus functies. De cosinus geeft de horizontale positie aan, en de sinus geeft de verticale positie aan. Dit principe wordt ook gebruikt in motoren, generatoren en vele andere machines.
Dit is waarom het zo belangrijk is: Het begrijpen van de relatie tussen circulaire beweging en goniometrie opent de deur naar het begrijpen van veel aspecten van de natuurkunde en techniek.
Tips om Sinus, Cosinus en Tangens te leren
Het leren van goniometrie hoeft niet eng te zijn. Hier zijn een paar tips om het makkelijker te maken:
- Begin met de basis: Zorg ervoor dat je de definities van sinus, cosinus en tangens goed begrijpt. Gebruik het ezelsbruggetje "SOS CAS TOA" om ze te onthouden.
- Oefen, oefen, oefen: Maak veel oefenopgaven. Hoe meer je oefent, hoe beter je het gaat begrijpen.
- Gebruik visuals: Zoek online naar afbeeldingen en animaties die de functies visualiseren. Dit kan je helpen om de concepten beter te begrijpen.
- Gebruik online hulpmiddelen: Er zijn veel online calculators en tools beschikbaar die je kunnen helpen bij het oplossen van goniometrische problemen.
- Zoek hulp: Als je er echt niet uitkomt, vraag dan hulp aan je docent, een tutor of een medestudent.
- Relateer het aan de realiteit: Probeer voorbeelden te vinden in je omgeving waar je deze functies kunt toepassen. Dit helpt bij het internaliseren van de concepten.
Voorbeeld oefening:
Stel: Je staat 50 meter van een flatgebouw. De hoek van elevatie naar de top van het gebouw is 35 graden. Wat is de hoogte van het gebouw?
Oplossing:
Gebruik de tangens functie: tan(35°) = hoogte / 50 meter
Hoogte = 50 * tan(35°)
Gebruik een calculator om tan(35°) te vinden: tan(35°) ≈ 0.700
Hoogte ≈ 50 * 0.700 = 35 meter
Dus de hoogte van het gebouw is ongeveer 35 meter.
Conclusie
Sinus, cosinus en tangens zijn krachtige tools die je kunnen helpen om problemen op te lossen in verschillende gebieden. Ze zijn essentieel voor navigatie, engineering, natuurkunde en nog veel meer. Hoewel ze in eerste instantie misschien intimiderend lijken, zijn ze eigenlijk heel toegankelijk als je ze stap voor stap leert.
Blijf oefenen, wees nieuwsgierig en durf vragen te stellen. Voor je het weet, zul je merken dat je deze functies moeiteloos kunt gebruiken om de wereld om je heen beter te begrijpen. En wie weet, misschien word je wel de volgende grote ingenieur of wetenschapper dankzij je kennis van goniometrie!
Dus, de volgende keer dat je sinus, cosinus of tangens tegenkomt, zie het dan niet als een obstakel, maar als een kans om iets nieuws te leren en je kennis te vergroten.
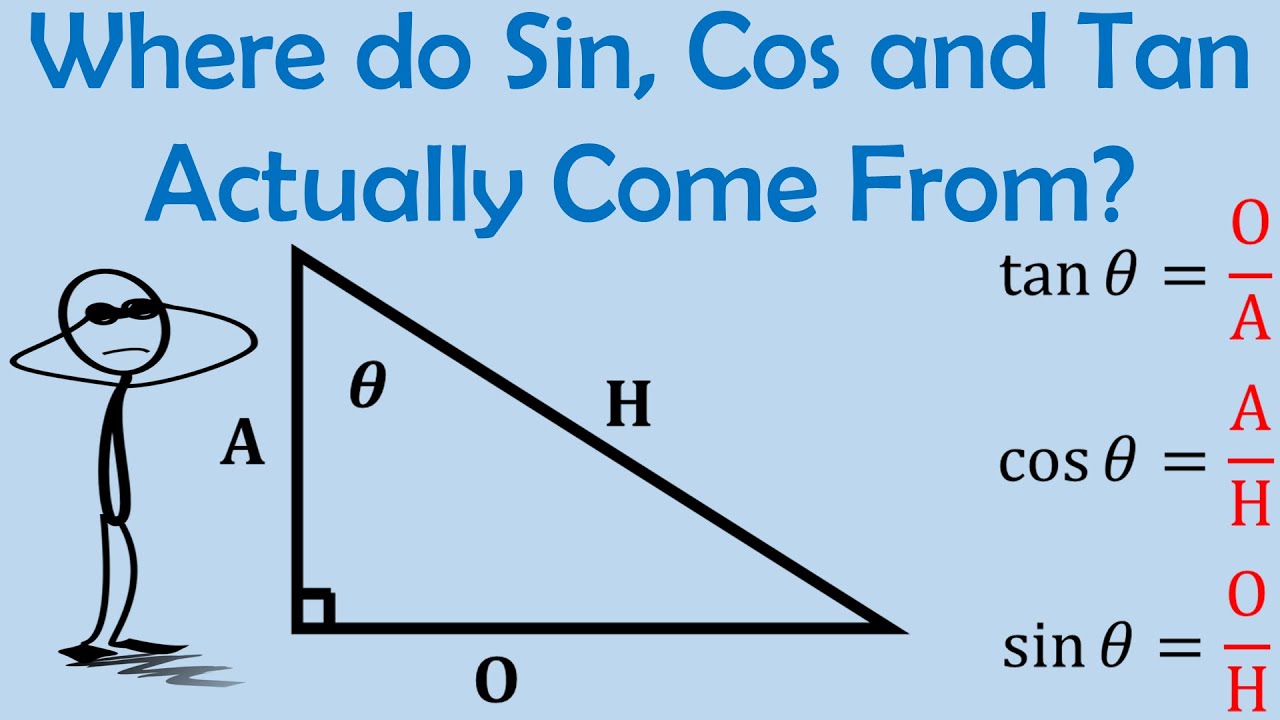
Bekijk ook deze gerelateerde berichten:
- Anne Van Der Bijl Overleden
- Verwachte N Term Geschiedenis Havo 2024
- Hoe Ga Je Naar De Hemel
- Afkorting Mevrouw In Het Engels
- Hoe Heet Het Witte In Je Oog
- 2 5 Mg Morfine Is Hoeveel Ml
- Eens Was Ik Een Vreemdeling Bladmuziek
- Waarom Heb Ik Dit Onderwerp Gekozen
- Wanneer Ben Je Verslaafd Aan Gamen
- Nieuw Nederlands Antwoorden 1 Havo/vwo
