Welke Statistische Toets Moet Ik Gebruiken

Stel je voor: je hebt wekenlang data verzameld, je zit vol enthousiasme achter je computer, maar dan... je staart naar die enorme dataset en vraagt je af: "Welke statistische toets moet ik in hemelsnaam gebruiken?" Herkenbaar? Geen zorgen, je bent zeker niet de enige. Het kiezen van de juiste statistische toets kan voelen als het navigeren door een doolhof. Deze gids is speciaal voor jou, de student, de onderzoeker, de data-analist in spe, die worstelt met deze cruciale vraag. We gaan samen de principes en overwegingen doornemen die je helpen de juiste beslissing te nemen, zodat je met vertrouwen je data kunt analyseren en betrouwbare conclusies kunt trekken.

Waarom is de juiste toets zo belangrijk?

Het kiezen van de juiste statistische toets is cruciaal voor een correcte interpretatie van je data. Een verkeerde toets kan leiden tot onjuiste conclusies, wat je hele onderzoek ongeldig kan maken. Denk bijvoorbeeld aan een arts die een verkeerde diagnose stelt. Dat kan serieuze gevolgen hebben, toch? In de statistiek is dat niet anders. Het is dus essentieel om te begrijpen hoe verschillende toetsen werken en wanneer je ze moet gebruiken.

Nauwkeurigheid: De juiste toets garandeert nauwkeurige resultaten en betrouwbare conclusies.
Validiteit: Het gebruik van een passende toets zorgt ervoor dat je onderzoek valide is en dat je bevindingen standhouden bij kritiek.
Tijdbesparing: Direct de juiste toets kiezen bespaart je tijd en frustratie in de lange run.
Vertrouwen: Met de juiste toets voel je je zelfverzekerd over je analyses en kun je je resultaten overtuigend presenteren.

De basis: Wat moet je weten voordat je begint?

Voordat we in de specifieke toetsen duiken, zijn er een paar belangrijke concepten die je moet begrijpen. Deze vormen de basis voor het maken van de juiste keuze:

1. Het Meetniveau van je Variabelen

Het meetniveau van je variabelen is een van de belangrijkste factoren bij het kiezen van een statistische toets. Er zijn vier meetniveaus:

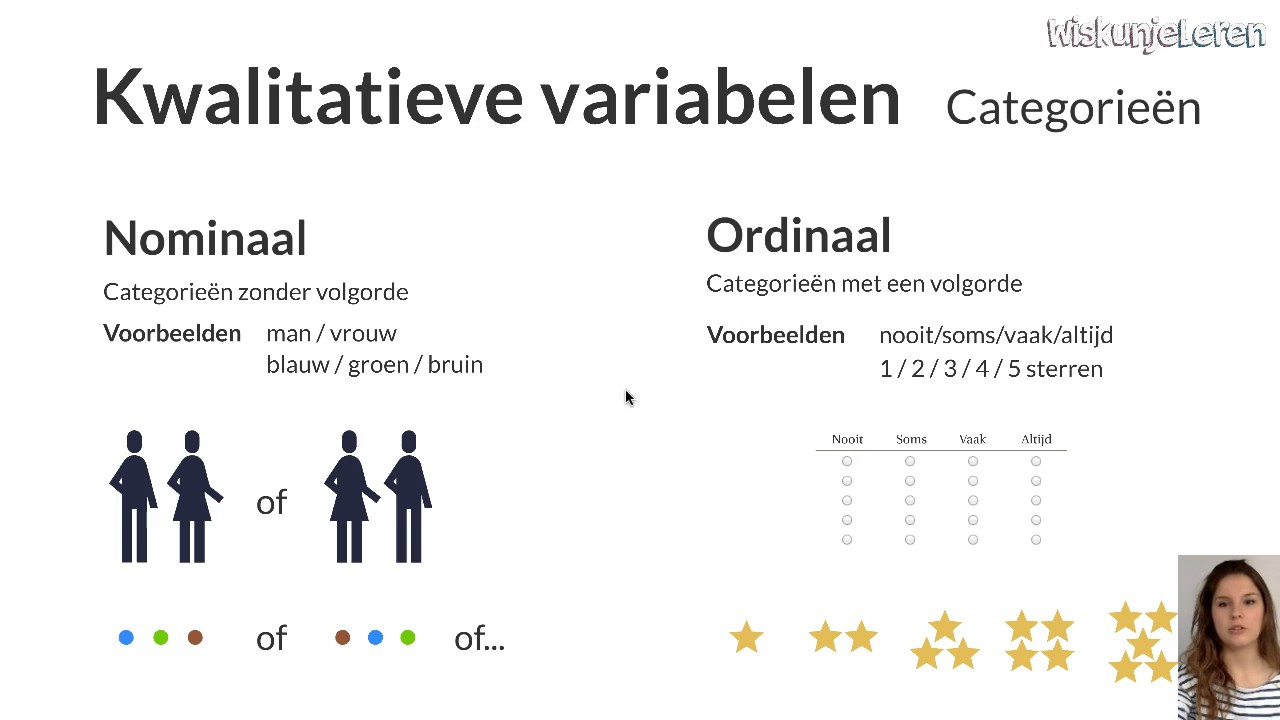
Nominaal: Categorieën zonder rangorde (bijvoorbeeld: geslacht, kleur, type auto). Je kunt ze labelen, maar niet ordenen.
Ordinaal: Categorieën met een rangorde, maar de verschillen tussen de categorieën zijn niet gedefinieerd (bijvoorbeeld: opleidingsniveau, Likert-schaal scores (helemaal mee oneens tot helemaal mee eens)). Je kunt zeggen dat het ene hoger is dan het andere, maar niet met hoeveel.
Interval: Gelijke intervallen tussen de waarden, maar geen absoluut nulpunt (bijvoorbeeld: temperatuur in Celsius of Fahrenheit). Je kunt verschillen berekenen, maar geen ratio's.
Ratio: Gelijke intervallen tussen de waarden en een absoluut nulpunt (bijvoorbeeld: leeftijd, gewicht, inkomen). Je kunt zowel verschillen als ratio's berekenen.

Waarom is dit belangrijk? Omdat bepaalde toetsen alleen geschikt zijn voor specifieke meetniveaus. Zo kun je bijvoorbeeld geen gemiddelde berekenen van nominale data.

2. De Onderzoeksvraag

Wat wil je eigenlijk weten? Je onderzoeksvraag is de leidraad voor je analyse. Formuleer je vraag helder en specifiek. Wil je:

Verschillen aantonen tussen groepen?
Een relatie onderzoeken tussen variabelen?
Een voorspelling doen op basis van een of meer variabelen?

De formulering van je onderzoeksvraag bepaalt welke type toets je nodig hebt.

3. De Verdeling van je Data

De verdeling van je data, ook wel distributie genoemd, is een ander cruciaal aspect. Is je data normaal verdeeld? Dit kun je visueel beoordelen met een histogram of Q-Q plot, of statistisch testen met bijvoorbeeld de Shapiro-Wilk test. Veel statistische toetsen, zoals de t-toets en ANOVA, zijn gebaseerd op de aanname van normaliteit. Als je data niet normaal verdeeld is, moet je mogelijk non-parametrische alternatieven overwegen.

Wat is een normale verdeling? Een normale verdeling is een symmetrische, klokvormige verdeling. Veel natuurlijke fenomenen volgen een normale verdeling.

4. Onafhankelijke vs. Afhankelijke Steekproeven

Zijn je steekproeven onafhankelijk van elkaar, of zijn ze gerelateerd? Bij onafhankelijke steekproeven zijn de waarnemingen in de ene groep niet gerelateerd aan de waarnemingen in de andere groep (bijvoorbeeld: een groep die een medicijn krijgt en een groep die een placebo krijgt). Bij afhankelijke steekproeven (ook wel gepaarde steekproeven genoemd) zijn de waarnemingen in de ene groep wel gerelateerd aan de waarnemingen in de andere groep (bijvoorbeeld: metingen van dezelfde persoon voor en na een interventie).

De meest gebruikte statistische toetsen: Een overzicht

Laten we nu eens kijken naar enkele van de meest gebruikte statistische toetsen en wanneer je ze kunt inzetten:

Verschillen tussen groepen

T-toets: Gebruik je om het gemiddelde van twee groepen te vergelijken.
- Onafhankelijke t-toets: Voor onafhankelijke steekproeven. Vereist normaliteit en gelijke varianties (kan getest worden met Levene's test).
- Gepaarde t-toets: Voor afhankelijke (gepaarde) steekproeven. Vereist normaliteit van de verschilscores.
ANOVA (Analysis of Variance): Gebruik je om het gemiddelde van meer dan twee groepen te vergelijken. Vereist normaliteit en gelijke varianties (kan getest worden met Levene's test). Er zijn verschillende soorten ANOVA, afhankelijk van je onderzoeksdesign.
Mann-Whitney U-toets (Wilcoxon rank-sum toets): Een non-parametrisch alternatief voor de onafhankelijke t-toets. Te gebruiken wanneer de data niet normaal verdeeld is. Vergelijkt de medianen van twee onafhankelijke groepen.
Wilcoxon signed-rank toets: Een non-parametrisch alternatief voor de gepaarde t-toets. Te gebruiken wanneer de data niet normaal verdeeld is. Vergelijkt de medianen van twee afhankelijke (gepaarde) groepen.
Kruskal-Wallis toets: Een non-parametrisch alternatief voor ANOVA. Te gebruiken wanneer de data niet normaal verdeeld is. Vergelijkt de medianen van meer dan twee onafhankelijke groepen.
Chi-kwadraattoets (Chi-square test): Gebruik je om de relatie tussen twee categorische variabelen te onderzoeken. Bijvoorbeeld: is er een verband tussen geslacht en stemgedrag?

Relaties tussen variabelen

Pearson correlatie: Meet de lineaire relatie tussen twee continue variabelen. Vereist normaliteit. De correlatiecoëfficiënt loopt van -1 tot +1.
Spearman correlatie: Een non-parametrische correlatie die de monotone relatie tussen twee variabelen meet. Te gebruiken wanneer de data niet normaal verdeeld is of wanneer je ordinale data hebt.
Regressieanalyse: Gebruik je om de relatie tussen een afhankelijke variabele en een of meer onafhankelijke variabelen te modelleren en te voorspellen. Er zijn verschillende soorten regressieanalyse, afhankelijk van het type afhankelijke variabele (lineaire regressie, logistische regressie, etc.).

Voorbeelden om het concreet te maken

Laten we een paar concrete voorbeelden bekijken:

Onderzoeksvraag: Is er een verschil in de gemiddelde score op een wiskundetoets tussen jongens en meisjes?
- Meetniveau: Wiskundetoets score (ratio), geslacht (nominaal)
- Mogelijke toetsen: Onafhankelijke t-toets (als de data normaal verdeeld is), Mann-Whitney U-toets (als de data niet normaal verdeeld is)
Onderzoeksvraag: Is er een relatie tussen het aantal uren studeren en het tentamencijfer?
- Meetniveau: Aantal uren studeren (ratio), tentamencijfer (ratio)
- Mogelijke toetsen: Pearson correlatie (als de data normaal verdeeld is), Spearman correlatie (als de data niet normaal verdeeld is)
Onderzoeksvraag: Is er een verband tussen de politieke voorkeur (links, rechts, midden) en het stemgedrag (wel of niet gestemd)?
- Meetniveau: Politieke voorkeur (nominaal), stemgedrag (nominaal)
- Mogelijke toets: Chi-kwadraattoets

Een stappenplan voor het kiezen van de juiste toets

Om het je makkelijker te maken, hier een stappenplan dat je kunt volgen:

Formuleer je onderzoeksvraag helder en specifiek. Wat wil je precies onderzoeken?
Bepaal het meetniveau van je variabelen. Zijn ze nominaal, ordinaal, interval of ratio?
Bepaal of je steekproeven onafhankelijk of afhankelijk zijn.
Controleer de verdeling van je data. Is je data normaal verdeeld?
Kies de toets die past bij je onderzoeksvraag, meetniveau, steekproeven en verdeling van de data. Gebruik de overzichten hierboven als leidraad.
Voer de toets uit met behulp van statistische software (bijvoorbeeld SPSS, R, Python).
Interpreteer de resultaten en trek conclusies.

Tips en tricks

Raadpleeg een statisticus of ervaren onderzoeker. Zeker als je twijfelt, is het altijd verstandig om advies te vragen.
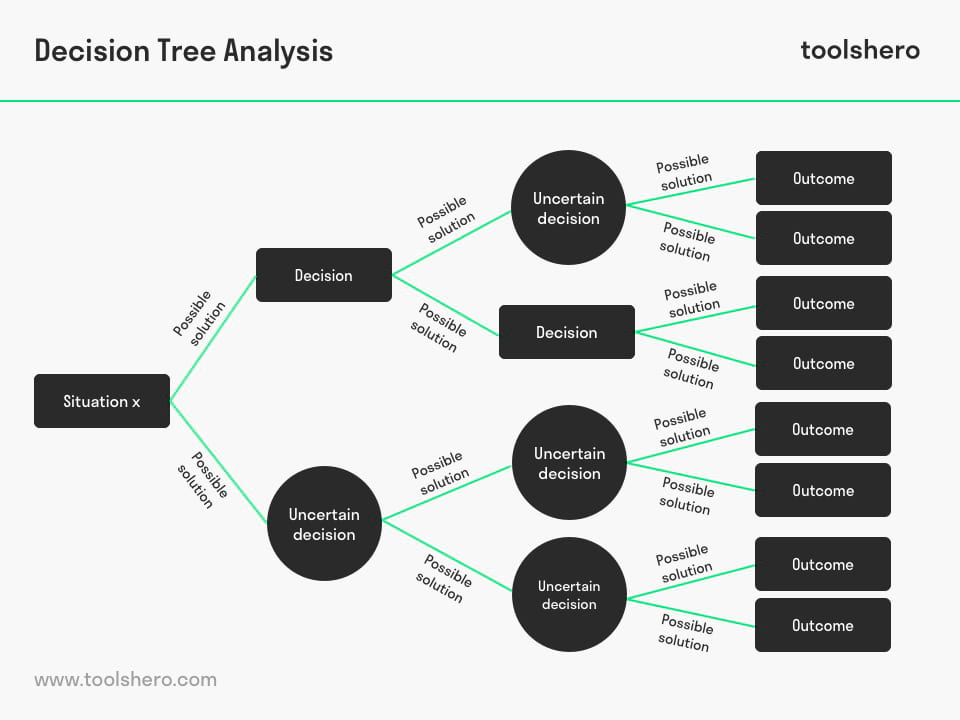
Gebruik online tools en decision trees. Er zijn verschillende online tools beschikbaar die je kunnen helpen bij het kiezen van de juiste toets.
Lees artikelen en boeken over statistiek. Hoe meer je weet over statistiek, hoe makkelijker het zal zijn om de juiste beslissingen te nemen.
Oefen, oefen, oefen! Hoe meer je oefent met het kiezen en uitvoeren van statistische toetsen, hoe beter je erin wordt.

Tot slot: Statistiek is een hulpmiddel, geen doel op zich

Onthoud dat statistiek een hulpmiddel is om je onderzoeksvraag te beantwoorden en betrouwbare conclusies te trekken. Het is geen doel op zich. Laat je niet overweldigen door de complexiteit van de verschillende toetsen, maar focus op het begrijpen van de principes en de logica erachter. Met de juiste kennis en aanpak kun je met vertrouwen je data analyseren en waardevolle inzichten ontdekken.

We hopen dat deze gids je heeft geholpen om meer inzicht te krijgen in de wereld van statistische toetsen. Succes met je onderzoek!