Gemiddelde N Term Wiskunde A Vwo

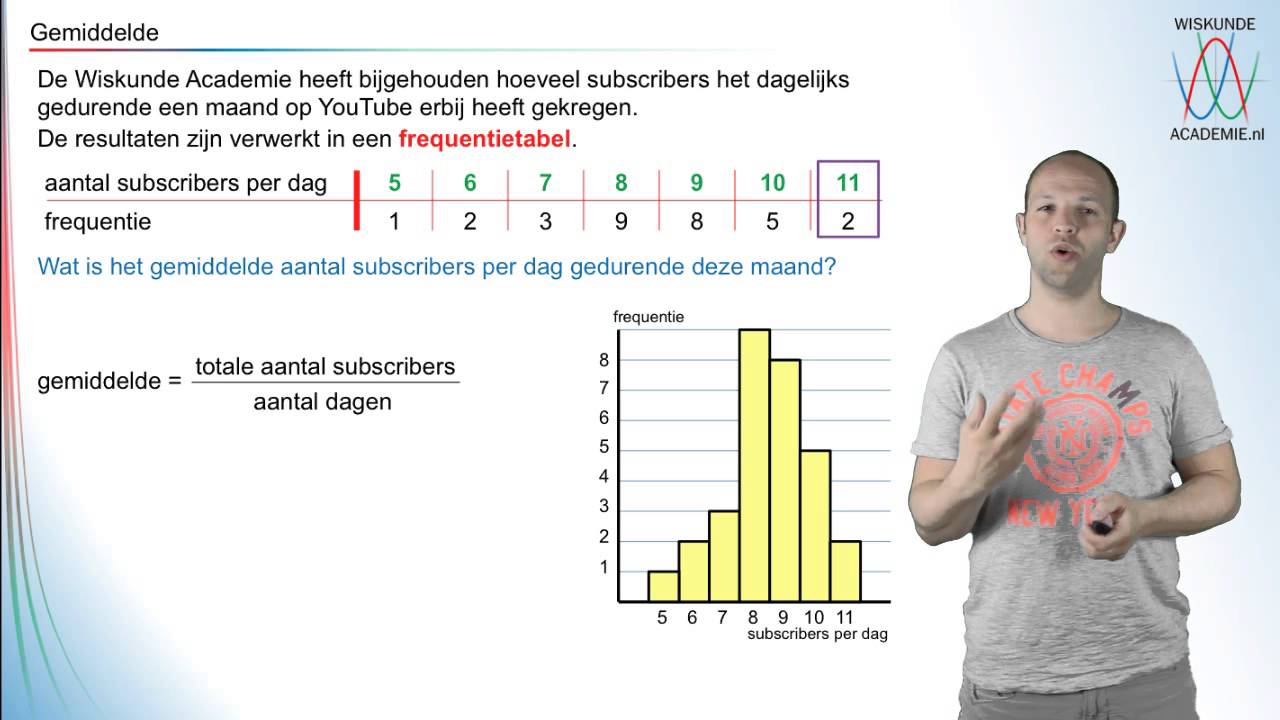
Heb je ooit vastgezeten bij een wiskunde A opgave, starend naar een breuk of een reeks cijfers, afvragend hoe je in hemelsnaam het gemiddelde aantal termen moest berekenen? Zo ja, dan ben je niet de enige. Dit artikel is speciaal geschreven voor VWO-leerlingen die worstelen met dit specifieke onderdeel van de wiskunde A stof. We gaan dieper in op wat het betekent, hoe je het berekent, en vooral, hoe je het kunt toepassen om je wiskunde A resultaten te verbeteren.

Wat is het Gemiddelde Aantal Termen eigenlijk?

Laten we beginnen met de basis. Het gemiddelde aantal termen, vaak aangeduid met 'n' in formules, is een concept dat vooral relevant is bij rijen en reeksen. Het vertegenwoordigt de 'typische' positie van een term in een reeks, vooral wanneer die reeks gebruikt wordt om een gemiddelde te bepalen. Dit is cruciaal bij het analyseren van data, financiële modellen, en andere toepassingen die je tegenkomt in wiskunde A.

Denk bijvoorbeeld aan een spaarrekening waar je maandelijks een bedrag stort. Om te berekenen hoeveel je na een bepaalde tijd hebt, moet je wellicht de som van een reeks berekenen. Het gemiddelde aantal termen helpt je dan om te bepalen over welke periode je het gemiddelde neemt.

Waarom is dit zo belangrijk?

Begrijpen van de context: Het helpt je om de context van een probleem beter te begrijpen.
Correcte berekeningen: Het zorgt ervoor dat je de juiste formules gebruikt en nauwkeurige antwoorden krijgt.
Probleemoplossend vermogen: Het scherpt je probleemoplossend vermogen aan, niet alleen in wiskunde, maar ook in andere vakken en het dagelijks leven.

Hoe bereken je het Gemiddelde Aantal Termen?

Er zijn verschillende manieren om het gemiddelde aantal termen te berekenen, afhankelijk van het type reeks dat je hebt. Laten we de meest voorkomende scenario's bekijken:

1. Rekenkundige Rijen

Een rekenkundige rij is een reeks getallen waarbij het verschil tussen opeenvolgende termen constant is. Bijvoorbeeld: 2, 4, 6, 8, 10...

De formule voor de som van een rekenkundige rij is:

S_n = (n/2) * (a₁ + a_n)

Waarbij:

S_n de som van de eerste 'n' termen is.
n het aantal termen is (dat wat we zoeken!).
a₁ de eerste term is.
a_n de laatste term is.

Hoe vinden we 'n'? Als je S_n, a₁ en a_n kent, kun je de formule omschrijven om 'n' te vinden:

n = (2 * S_n) / (a₁ + a_n)

Voorbeeld: Stel, de som van een rekenkundige rij is 55, de eerste term is 1 en de laatste term is 10. Dan is n = (2 * 55) / (1 + 10) = 110 / 11 = 10. Dus het gemiddelde aantal termen is 10.

2. Meetkundige Rijen

Een meetkundige rij is een reeks getallen waarbij elke term wordt verkregen door de vorige term te vermenigvuldigen met een constante factor (de reden). Bijvoorbeeld: 2, 4, 8, 16, 32...

De formule voor de som van een meetkundige rij is:

S_n = a₁ * (1 - rⁿ) / (1 - r)

Waarbij:

S_n de som van de eerste 'n' termen is.
n het aantal termen is (weer wat we zoeken!).
a₁ de eerste term is.
r de reden is (de constante factor).

Hoe vinden we 'n'? Het vinden van 'n' in een meetkundige rij is iets lastiger omdat 'n' in de exponent staat. Je hebt vaak logaritmen nodig om dit op te lossen. De formule kan worden omgeschreven, maar dit kan complex zijn, afhankelijk van de gegevens die je hebt. Soms is het handiger om te gokken en te checken, vooral als 'n' een geheel getal moet zijn.

Voorbeeld: Stel, de som van een meetkundige rij is 31, de eerste term is 1 en de reden is 2. Dan is 31 = 1 * (1 - 2ⁿ) / (1 - 2). Dit vereenvoudigt tot 31 = (1 - 2ⁿ) / -1, wat verder gaat als -31 = 1 - 2ⁿ. Dus 2ⁿ = 32. Hieruit volgt dat n = 5. Dus het gemiddelde aantal termen is 5.

3. Complexe Scenario's

Soms kom je situaties tegen waarbij de rij niet direct rekenkundig of meetkundig is. In deze gevallen kan het nodig zijn om de rij eerst te analyseren en te proberen een patroon te ontdekken. Soms kun je de rij opsplitsen in twee of meer rijen die je wel kunt analyseren.

Praktische Toepassingen in Wiskunde A

Het concept van het gemiddelde aantal termen duikt op in verschillende contexten binnen wiskunde A:

Financiële wiskunde: Bij het berekenen van de waarde van een annuïteit of een lening.
Statistiek: Bij het analyseren van reeksen data en het berekenen van gemiddelden over bepaalde periodes.
Modelleren: Bij het opstellen van modellen voor groei of afname, bijvoorbeeld bij populatiemodellen.
Kansrekening: Bij het berekenen van de verwachte waarde van een reeks gebeurtenissen.

Voorbeeld Financiële Wiskunde: Stel je voor dat je een lening afsluit die je in 60 maandelijkse termijnen terugbetaalt. De rente is vast. Om de totale rente te berekenen, kun je de som van een rekenkundige rij gebruiken, waarbij het gemiddelde aantal termen (n) 60 is.

Tips en Tricks voor het Oefenen

Hier zijn enkele tips om je vaardigheden in het berekenen van het gemiddelde aantal termen te verbeteren:

Oefen, oefen, oefen: Maak zoveel mogelijk opgaven. Hoe meer je oefent, hoe beter je de verschillende typen rijen en reeksen herkent.
Gebruik voorbeelden: Bestudeer uitgewerkte voorbeelden in je leerboek of online. Probeer ze zelf na te rekenen.
Begrijp de formules: Onthoud de formules niet alleen, maar begrijp ook waar ze vandaan komen.
Zoek hulp: Vraag je docent, een medeleerling of een tutor om hulp als je vastzit.
Gebruik online tools: Er zijn veel online calculators en resources beschikbaar die je kunnen helpen bij het controleren van je antwoorden.

Maak het Relateerbaar: Een Persoonlijke Aanpak

Wiskunde kan soms abstract aanvoelen. Probeer het concept van het gemiddelde aantal termen te relateren aan je eigen leven. Denk bijvoorbeeld aan:

Sparen: Hoe lang duurt het voordat je een bepaald bedrag hebt gespaard?
Sport: Hoeveel trainingen heb je nodig om je doel te bereiken?
School: Hoeveel uur per week besteed je aan wiskunde?

Door wiskunde te verbinden met je eigen ervaringen, wordt het niet alleen interessanter, maar ook makkelijker te begrijpen.

Conclusie: Meer dan alleen Cijfers

Het berekenen van het gemiddelde aantal termen is meer dan alleen het toepassen van een formule. Het is een manier om patronen te herkennen, problemen op te lossen en de wereld om je heen beter te begrijpen. Door de principes achter rijen en reeksen te begrijpen, ontwikkel je vaardigheden die je niet alleen in de wiskundeles, maar ook in je verdere studie en carrière van pas zullen komen.

Dus, de volgende keer dat je een opgave tegenkomt met een reeks, haal diep adem, herinner je de formules, en bovenal, vertrouw op je eigen kunnen. Met de juiste aanpak en voldoende oefening kun je dit onderdeel van wiskunde A zeker onder de knie krijgen. Succes!