Hoe Bereken Ik Een Oppervlakte

Het berekenen van een oppervlakte is een essentiële vaardigheid die in talloze aspecten van ons dagelijks leven terugkomt. Of je nu een huis wilt kopen, een tuin wilt aanleggen, een kamer wilt schilderen of gewoon nieuwsgierig bent naar de afmetingen van een object, kennis van oppervlakteberekening is onmisbaar. Dit artikel biedt een uitgebreide gids over hoe je de oppervlakte van verschillende vormen kunt berekenen, waarbij we duidelijke uitleg, voorbeelden en praktische toepassingen zullen behandelen.

Wat is Oppervlakte Eigenlijk?

Oppervlakte is de maat van een tweedimensionaal (2D) gebied. Het wordt uitgedrukt in vierkante eenheden, zoals vierkante meters (m²), vierkante centimeters (cm²), vierkante kilometers (km²) of vierkante voet (ft²). Denk erover na als het aantal eenheden van een bepaald formaat (bijvoorbeeld vierkante meters) dat nodig is om een platte figuur volledig te bedekken.

Waarom is Oppervlakteberekening Belangrijk?

De vaardigheid om oppervlaktes te berekenen is cruciaal in veel verschillende situaties:

• Huis en Tuin: Bij de aankoop of verkoop van een huis is de oppervlakte van het perceel en de woonruimte van groot belang. Het helpt ook bij het bepalen van de benodigde hoeveelheid verf, vloerbedekking of tuinaarde.
• Bouw en Architectuur: Architecten en bouwers gebruiken oppervlakteberekeningen om materialen te schatten, plattegronden te ontwerpen en de kosten van projecten te bepalen.
• Landmeten: Landmeters gebruiken geavanceerde technieken om de oppervlakte van land te bepalen, wat essentieel is voor eigendomsgrenzen, landgebruik en belastingen.
• Wiskunde en Wetenschap: Oppervlakteberekening is een fundamenteel concept in de wiskunde en wordt gebruikt in verschillende wetenschappelijke disciplines, zoals natuurkunde en engineering.

De Basisformules voor Oppervlakte

Laten we de formules bekijken voor het berekenen van de oppervlakte van enkele veelvoorkomende geometrische vormen:

1. Rechthoek en Vierkant

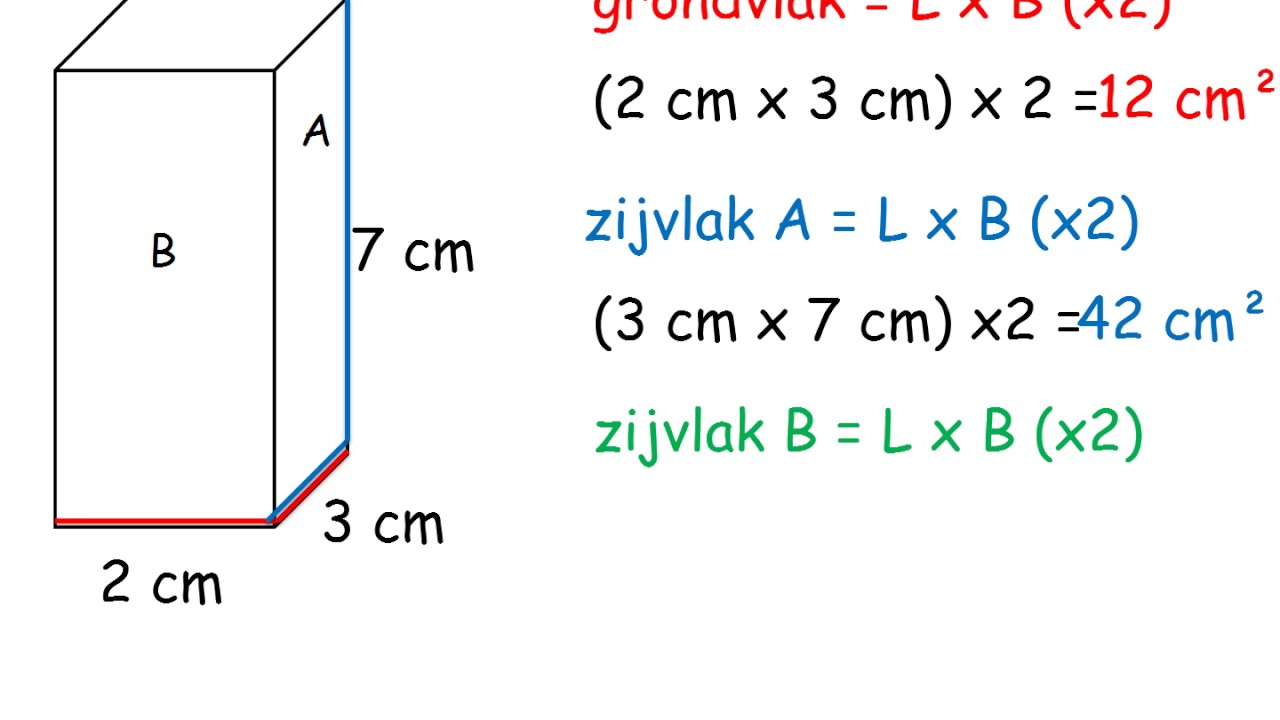
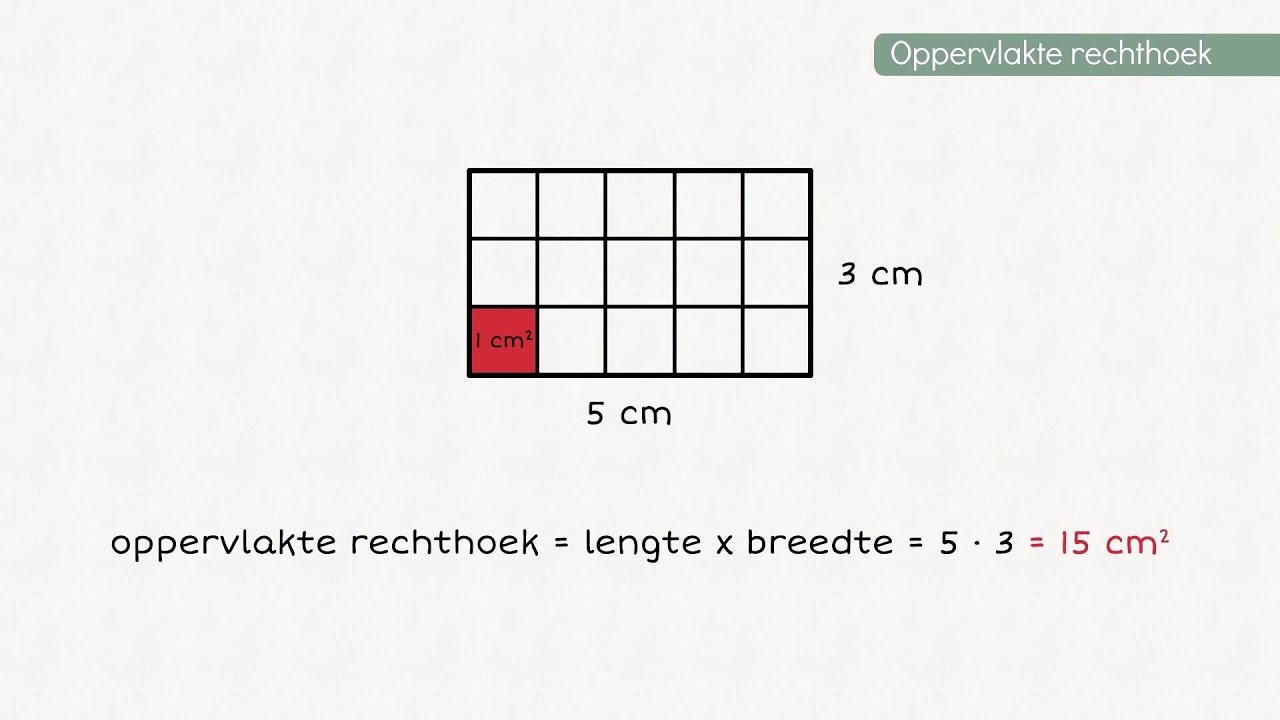
Een rechthoek is een vierhoek met vier rechte hoeken. De oppervlakte van een rechthoek wordt berekend door de lengte te vermenigvuldigen met de breedte:

Oppervlakte = Lengte x Breedte

Een vierkant is een speciale rechthoek waarbij alle zijden gelijk zijn. Dus de oppervlakte van een vierkant is:

Oppervlakte = Zijde x Zijde = Zijde²

Voorbeeld: Een rechthoekige kamer is 5 meter lang en 4 meter breed. De oppervlakte is 5 m x 4 m = 20 m².

2. Driehoek

De oppervlakte van een driehoek wordt berekend door de basis te vermenigvuldigen met de hoogte en vervolgens te delen door 2:

Oppervlakte = (Basis x Hoogte) / 2

De basis is een van de zijden van de driehoek en de hoogte is de loodrechte afstand van de basis tot de tegenoverliggende hoekpunt.

Voorbeeld: Een driehoek heeft een basis van 8 cm en een hoogte van 6 cm. De oppervlakte is (8 cm x 6 cm) / 2 = 24 cm².

3. Cirkel

De oppervlakte van een cirkel wordt berekend met behulp van de straal (de afstand van het middelpunt tot de rand) en de wiskundige constante pi (π ≈ 3,14159):

Oppervlakte = π x Straal²

Voorbeeld: Een cirkel heeft een straal van 3 meter. De oppervlakte is π x (3 m)² ≈ 3,14159 x 9 m² ≈ 28,27 m².

4. Parallellogram

Een parallellogram is een vierhoek met twee paar evenwijdige zijden. De oppervlakte wordt berekend door de basis te vermenigvuldigen met de hoogte:

Oppervlakte = Basis x Hoogte

De hoogte is de loodrechte afstand tussen de basis en de tegenoverliggende zijde.

Voorbeeld: Een parallellogram heeft een basis van 10 cm en een hoogte van 5 cm. De oppervlakte is 10 cm x 5 cm = 50 cm².

5. Trapezium

Een trapezium (of trapezoïde) is een vierhoek met ten minste één paar evenwijdige zijden. De oppervlakte wordt berekend door de som van de evenwijdige zijden te vermenigvuldigen met de hoogte en vervolgens te delen door 2:

Oppervlakte = ((Zijde A + Zijde B) x Hoogte) / 2

Zijde A en Zijde B zijn de evenwijdige zijden, en de hoogte is de loodrechte afstand tussen deze zijden.

Voorbeeld: Een trapezium heeft evenwijdige zijden van 6 cm en 8 cm, en een hoogte van 4 cm. De oppervlakte is ((6 cm + 8 cm) x 4 cm) / 2 = 28 cm².

Complexe Vormen en Oppervlakteberekening

In de praktijk kom je vaak complexe vormen tegen die niet direct passen in de bovenstaande categorieën. Om de oppervlakte van deze vormen te berekenen, zijn er verschillende strategieën:

1. Decompositie: Verdeel de complexe vorm in eenvoudigere vormen (rechthoeken, driehoeken, cirkels) waarvan je de oppervlakte wel kunt berekenen. Tel vervolgens de oppervlaktes van de individuele vormen bij elkaar op.
2. Benadering: Gebruik een raster (een netwerk van vierkanten) om de oppervlakte te benaderen. Tel de vierkanten die volledig binnen de vorm liggen, en schat de oppervlakte van de vierkanten die gedeeltelijk binnen de vorm liggen.
3. Integrale Rekening (Calculus): Voor meer complexe vormen kan integrale rekening worden gebruikt om de oppervlakte exact te bepalen. Dit is een geavanceerde techniek die buiten het bestek van deze introductie valt.
4. Software en Tools: Er zijn diverse softwarepakketten en online tools beschikbaar die je kunnen helpen bij het berekenen van de oppervlakte van complexe vormen, vaak op basis van een afbeelding of schets.

Een Praktisch Voorbeeld: De Oppervlakte van een Kamer met een Erker

Stel, je wilt de oppervlakte berekenen van een kamer met een rechthoekige basis en een halfcirkelvormige erker. De rechthoekige basis is 5 meter lang en 4 meter breed. De erker heeft een diameter van 2 meter (dus een straal van 1 meter).

1. Bereken de oppervlakte van de rechthoek: 5 m x 4 m = 20 m²
2. Bereken de oppervlakte van de halve cirkel: (π x (1 m)²) / 2 ≈ (3,14159 x 1 m²) / 2 ≈ 1,57 m²
3. Tel de oppervlaktes bij elkaar op: 20 m² + 1,57 m² = 21,57 m²

De totale oppervlakte van de kamer is dus ongeveer 21,57 m².

Belangrijke Tips en Aandachtspunten

• Gebruik de juiste eenheden: Zorg ervoor dat alle metingen in dezelfde eenheden zijn (bijvoorbeeld allemaal in meters of allemaal in centimeters) voordat je de oppervlakte berekent.
• Rond af: Rond je antwoord af op een redelijk aantal decimalen, afhankelijk van de nauwkeurigheid die nodig is.
• Controleer je antwoord: Controleer je antwoord door een schatting te maken of door de berekening opnieuw uit te voeren.
• Gebruik een rekenmachine: Gebruik een rekenmachine om fouten te voorkomen, vooral bij ingewikkelde berekeningen.
• Begrijp de concepten: Het is belangrijk om de concepten achter de formules te begrijpen, in plaats van ze alleen maar uit je hoofd te leren. Dit helpt je om problemen op te lossen en om de juiste formule te kiezen voor de situatie.

Real-World Voorbeelden en Data

Laten we eens kijken naar enkele real-world voorbeelden waarin oppervlakteberekening van cruciaal belang is:

• Zonnepanelen: Het oppervlak van zonnepanelen bepaalt hoeveel zonlicht ze kunnen opvangen en dus hoeveel energie ze kunnen genereren. Het optimaliseren van het oppervlak van zonnepaneelinstallaties is essentieel voor maximale energieopbrengst.
• Landbouw: Boeren gebruiken oppervlakteberekeningen om de hoeveelheid landbouwgrond te bepalen die ze bezitten of bewerken. Dit is belangrijk voor het plannen van gewassen, het toedienen van meststoffen en het schatten van de oogst.
• Verpakking: De oppervlakte van verpakkingsmateriaal (zoals karton) is belangrijk voor het bepalen van de kosten van de verpakking en voor het minimaliseren van afval.
• Medische Beeldvorming: In de medische wereld wordt oppervlakteberekening gebruikt om de grootte van tumoren of andere afwijkingen te bepalen, wat essentieel is voor de diagnose en behandeling van ziekten.

Conclusie

Het berekenen van de oppervlakte is een waardevolle vaardigheid die je in talloze situaties kunt gebruiken. Door de basisformules te leren, complexe vormen te ontleden en de nodige voorzorgsmaatregelen te nemen, kun je de oppervlakte van vrijwel elke 2D-vorm nauwkeurig bepalen. Of je nu een professional bent in de bouw, architectuur, landmeten of gewoon een alledaagse klusser, het beheersen van oppervlakteberekening zal je zeker van pas komen.

Oefen de verschillende methoden en formules die in dit artikel zijn beschreven. Begin met eenvoudige vormen en ga geleidelijk over naar complexere vormen. Gebruik real-world voorbeelden om je kennis te testen en je vaardigheden te verbeteren. Met oefening en geduld zul je al snel een expert worden in oppervlakteberekening!