N Termen Wiskunde B Vwo

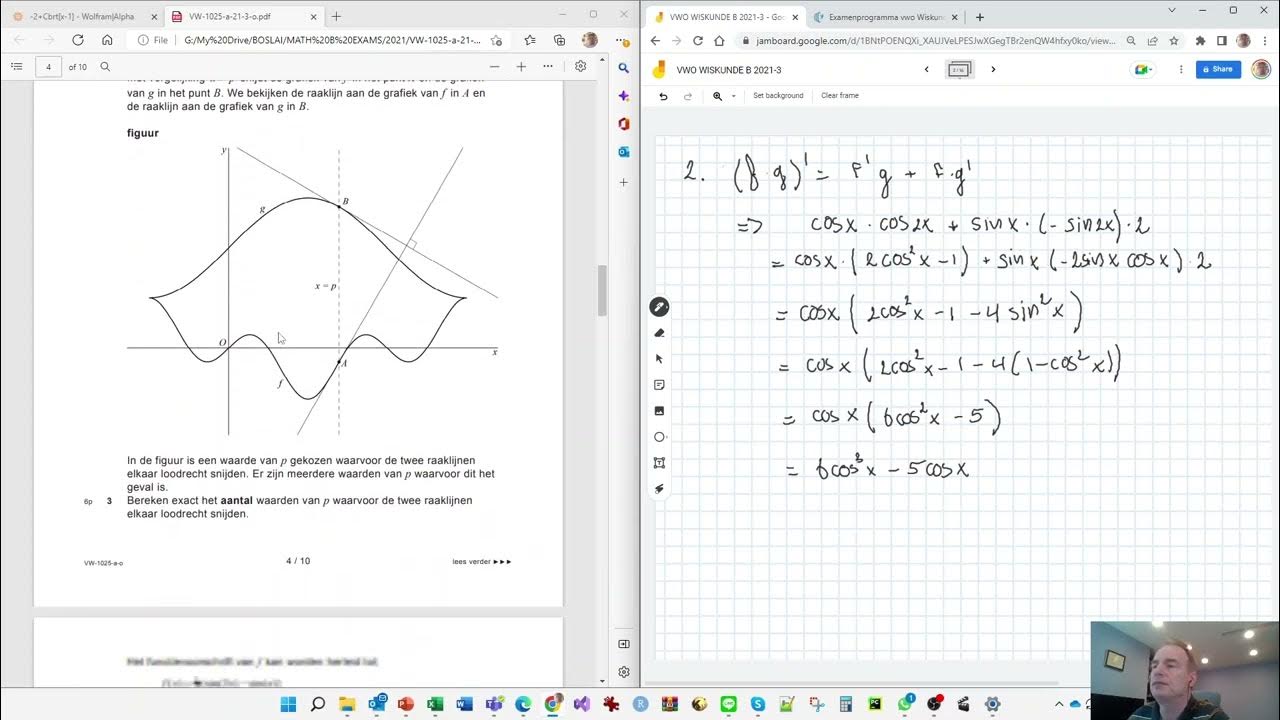
Wiskunde B VWO, voor velen een uitdaging, voor sommigen een passie. Het is een vak dat verder reikt dan alleen maar getallen en formules. Het leert je logisch denken, problemen oplossen en abstract redeneren. In dit artikel duiken we dieper in op de belangrijkste aspecten van N-termen in Wiskunde B VWO. We zullen de sleutelconcepten bespreken, de relevantie aantonen en concrete voorbeelden geven. Het doel is om een helder en inzichtelijk overzicht te bieden, zonder de complexiteit van de materie te bagatelliseren.

Wat zijn N-termen?

De term "N-termen" verwijst niet naar een specifiek wiskundig onderwerp binnen Wiskunde B VWO, maar is eerder een informele aanduiding voor nieuwe of complexere onderwerpen die leerlingen tijdens hun studie tegenkomen. Het omvat doorgaans onderwerpen die verder bouwen op de basisprincipes en meer abstracte denkwijzen vereisen. Deze "N-termen" kunnen per leerjaar variëren, afhankelijk van het leerplan en de specifieke school.

Over het algemeen omvatten N-termen in Wiskunde B VWO onderwerpen als:

Complexe getallen: Rekenen met getallen die een reëel en imaginair deel bevatten.
Differentiaalvergelijkingen: Vergelijkingen waarin een functie en haar afgeleiden voorkomen.
Integratietechnieken: Geavanceerde methoden om integralen te berekenen, zoals partiële integratie en substitutie.
Bewijzen: Formeel aantonen van wiskundige stellingen.
Vectorrekening: Werken met vectoren in de twee- en driedimensionale ruimte.
Meetkunde: Diepgaande analyse van meetkundige figuren en hun eigenschappen.

Waarom zijn N-termen belangrijk?

Het beheersen van deze "N-termen" is essentieel om meerdere redenen:

Voorbereiding op het hoger onderwijs: Veel studies in het technische, wetenschappelijke en economische domein vereisen een sterke basis in Wiskunde B. Deze onderwerpen komen vaak terug in de eerste jaren van een universitaire of HBO-opleiding.
Ontwikkeling van abstract denkvermogen: Het bestuderen van deze complexere onderwerpen stimuleert de ontwikkeling van abstract denkvermogen, wat van cruciaal belang is voor het oplossen van complexe problemen in diverse disciplines.
Verbeteren van probleemoplossende vaardigheden: N-termen vereisen vaak een creatieve en analytische aanpak. Het succesvol doorlopen van deze opgaven helpt leerlingen om hun probleemoplossende vaardigheden te verbeteren.
Verdieping van wiskundig inzicht: Het is niet enkel reproduceren van formules, maar het begrijpen van de onderliggende principes. Dit leidt tot een dieper wiskundig inzicht, waardoor leerlingen beter in staat zijn om nieuwe en uitdagende problemen aan te pakken.

Dieper ingaan op enkele N-termen

Complexe getallen

Complexe getallen, bestaande uit een reëel en een imaginair deel (a + bi), lijken in eerste instantie misschien abstract en irrelevant. Echter, ze spelen een cruciale rol in diverse gebieden van de wetenschap en technologie. In de elektrotechniek worden ze gebruikt om wisselstroomcircuits te analyseren. In de kwantummechanica zijn ze essentieel voor het beschrijven van de golffunctie van deeltjes. Ook in de signaalverwerking worden complexe getallen gebruikt voor de analyse en manipulatie van signalen.

Een praktisch voorbeeld: Stel je voor dat je een elektrisch circuit analyseert met weerstanden, condensatoren en spoelen. Met behulp van complexe getallen kun je de impedantie (de weerstand tegen wisselstroom) van elk element beschrijven en vervolgens de totale stroom en spanning in het circuit berekenen. Dit zou onmogelijk zijn met alleen reële getallen.

Differentiaalvergelijkingen

Differentiaalvergelijkingen beschrijven de relatie tussen een functie en haar afgeleiden. Ze worden gebruikt om processen te modelleren die in de tijd veranderen, zoals de groei van een populatie, de beweging van een object of de verspreiding van een ziekte. Het oplossen van differentiaalvergelijkingen kan complex zijn, maar de resultaten geven waardevolle inzichten in de dynamiek van deze processen.

Een voorbeeld: Stel je voor dat je de groei van een bacteriekolonie wilt modelleren. Met behulp van een differentiaalvergelijking kun je beschrijven hoe de groeisnelheid afhangt van de huidige populatiegrootte. Door de vergelijking op te lossen, kun je voorspellen hoe de populatie in de toekomst zal groeien, rekening houdend met factoren als voedselbeschikbaarheid en competitie.

Integratietechnieken

Integratietechnieken, zoals partiële integratie en substitutie, zijn geavanceerde methoden om integralen te berekenen. Integralen worden gebruikt om de oppervlakte onder een curve te bepalen, maar ze hebben ook bredere toepassingen. Ze worden gebruikt om de kansdichtheid van een continue variabele te berekenen, de arbeid die door een kracht wordt verricht, of het volume van een driedimensionaal object.

Een voorbeeld: Stel je voor dat je de totale energie wilt berekenen die een zonnepaneel gedurende een dag opvangt. Je kunt de vermogensopbrengst van het zonnepaneel als functie van de tijd meten en vervolgens de integraal van deze functie over de dag berekenen. Dit geeft je de totale energie die het zonnepaneel heeft opgevangen.

Tips voor het leren van N-termen

Het leren van "N-termen" kan een uitdaging zijn, maar met de juiste aanpak is het zeker haalbaar. Hier zijn enkele tips:

Zorg voor een sterke basis: Zorg ervoor dat je de basisconcepten van Wiskunde B goed beheerst voordat je aan complexere onderwerpen begint.
Oefen veel: Wiskunde leer je door te doen. Maak veel oefenopgaven en probeer verschillende benaderingen.
Zoek hulp: Aarzel niet om hulp te vragen aan je docent, medeleerlingen of een bijlesdocent als je vastloopt.
Begrijp de concepten: Probeer de onderliggende principes te begrijpen in plaats van alleen maar formules uit je hoofd te leren.
Visualiseer de concepten: Maak gebruik van diagrammen, grafieken en animaties om de concepten te visualiseren en beter te begrijpen.
Werk samen: Werk samen met medeleerlingen aan opgaven en bespreek de verschillende aanpakken.
Wees geduldig: Het leren van complexere onderwerpen kost tijd en moeite. Wees geduldig en geef niet op.

Conclusie

De "N-termen" in Wiskunde B VWO zijn essentiële bouwstenen voor een succesvolle toekomst in het hoger onderwijs en diverse professionele velden. Ze dagen je uit om dieper na te denken, analytisch te redeneren en creatieve oplossingen te vinden. Door deze uitdagingen aan te gaan en je te focussen op een sterke basis, veel oefening en hulp zoeken wanneer nodig, zul je niet alleen je wiskundige vaardigheden verbeteren, maar ook je algemene probleemoplossende vaardigheden ontwikkelen. Investeer in je wiskundige kennis, want het opent deuren naar een wereld vol mogelijkheden. Blijf vragen stellen, oefenen en leren, en je zult versteld staan van wat je kunt bereiken. Gebruik deze kennis om de wereld om je heen beter te begrijpen en een positieve impact te maken. Succes!